概述
大型语言模型 (Large Language Model,LLM) 生成领域的新训练范式:RLHF (Reinforcement Learning from Human Feedback) ,即以强化学习方式依据人类反馈优化语言模型。
RLHF 的意义在于能够结合人类的偏好与强化技术,对模型的输出进行优化,使模型更加符合人类期望,避免传统训练方法中问题,如:输出仅考虑语法的正确性和连贯性,但是不考虑合理性,会导致无意义回答以及牛头不对马嘴;输出没法满足各类规则/价值观的约束。
RLHF通过reward model将人类反馈融入训练过程中,基于强化学习策略优化策略,使训练的结果更加符合用户需求,同时也能更快适配新场景。
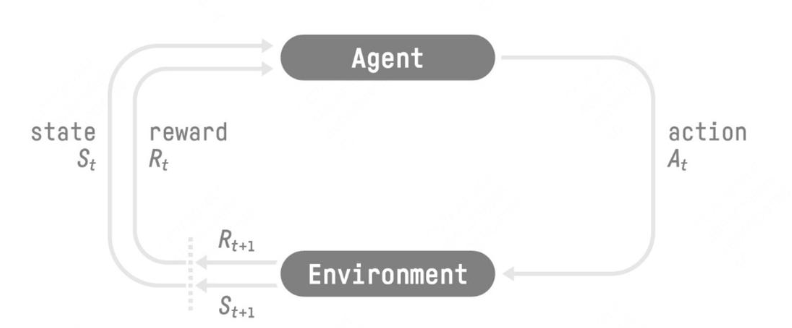
强化学习(RL)包括几个组成部分:
- 状态空间:状态空间是当前任务的所有可用信息,这些信息与 AI 代理可能做出的决策相关,包括已知和未知变量。状态空间通常会随着代理做出的每个决策而变化。
- 操纵空间:操作空间包含 AI 代理可能做出的所有决策。例如,在棋类游戏中,操作空间是离散且明确定义的:它由 AI 玩家在给定时刻可以采取的所有合法移动操作组成。在文本生成任务中,操作空间非常巨大,包括 LLM 可用的整个
token词汇表。 - 奖励函数:奖励是激励 AI 代理的成功或进步的衡量标准。在某些情况下,例如棋盘游戏,成功的定义(在本例中为赢得游戏)是客观且直接的。但是,当“成功”的定义模糊不清时,设计有效的奖励函数可能是一项重大挑战。在数学框架中,这种反馈必须转化为奖励信号:正(或负)反馈的标量量化。
- 约束条件:奖励函数可以通过惩罚(负奖励)来补充,也就是惩罚那些被认为对当前任务产生反作用的行为。例如,企业可能希望禁止聊天机器人使用脏话或其他粗俗语言;自动驾驶汽车模型可能会因碰撞或偏离车道而受到惩
- 政策:本质上,策略是驱动 AI 代理行为的策略或“思维过程”。用简单的数学术语来说,策略 (“π”) 是一个以状态 (“s”) 作为输入并返回动作 (“a”) 的函数:π(s)→a。
算法框架
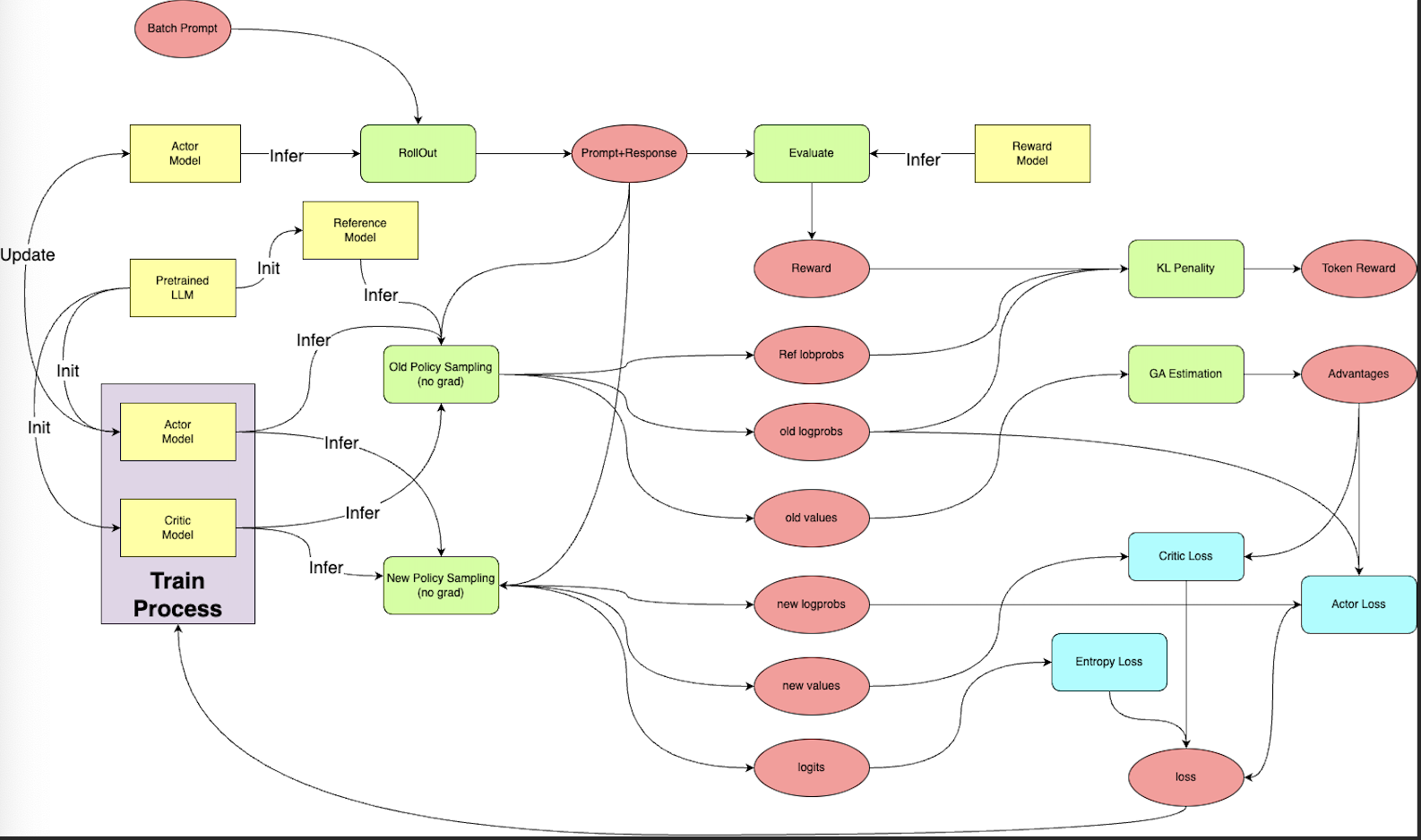
基于RLHF训练LLM的训练框架主要分为几个部分:
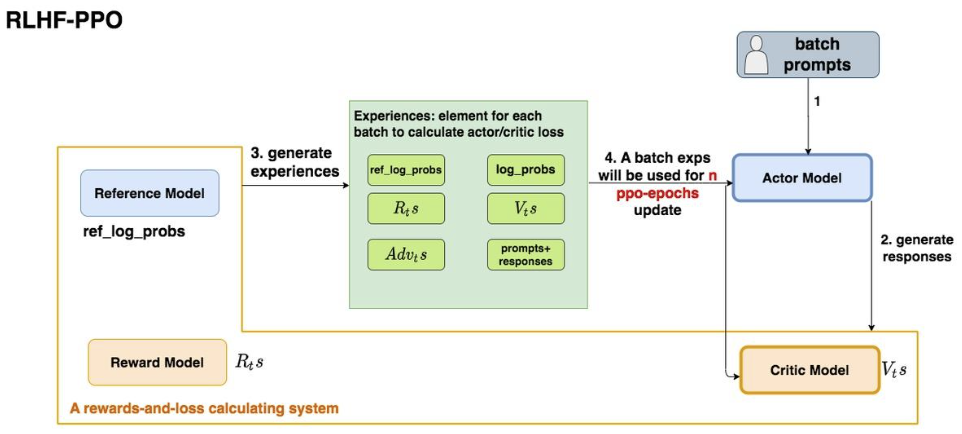
Actor Model需要训练。
Actor Model对应需要最终训练得到的目标语言模型。通过奖励信号(由Reward Model提供)和策略优化算法(如PPO)不断更新策略。通常采用预训练得到LLM模型进行初始化。Critic Model需要训练。
Critic Model用于估计给定状态的价值(Value Function)。在Actor-Critic强化学习框架中,Critic Model辅助Actor Model,通过计算优势函数指导策略更新。Reward Model不需要训练,提前训练好。
奖励模型用于评价生成的结果,量化其质量并引导策略优化,是 RLHF 的核心,直接决定了强化学习的优化目标。需要提前训练,通常有不同维度:安全、价值观评价、合理性等。
Reference Model不需要训练,提前训练好。
\[D_{\text{KL}}(P \| Q) = \sum_x P(x) \log \frac{P(x)}{Q(x)}\]Reference Model是训练过程中的对照基线,用于限制Actor Model的行为偏离预训练模型过多。它提供新旧策略的对比,通常用来计算 KL 散度约束。P 通常是当前策略 $\pi_\theta$ 的分布(
Actor Model)。Q 通常是基准策略 $\pi_{\text{reference}}$ 的分布(
Reference Model)。
利用RLHF训练LLM通常分为以下阶段:
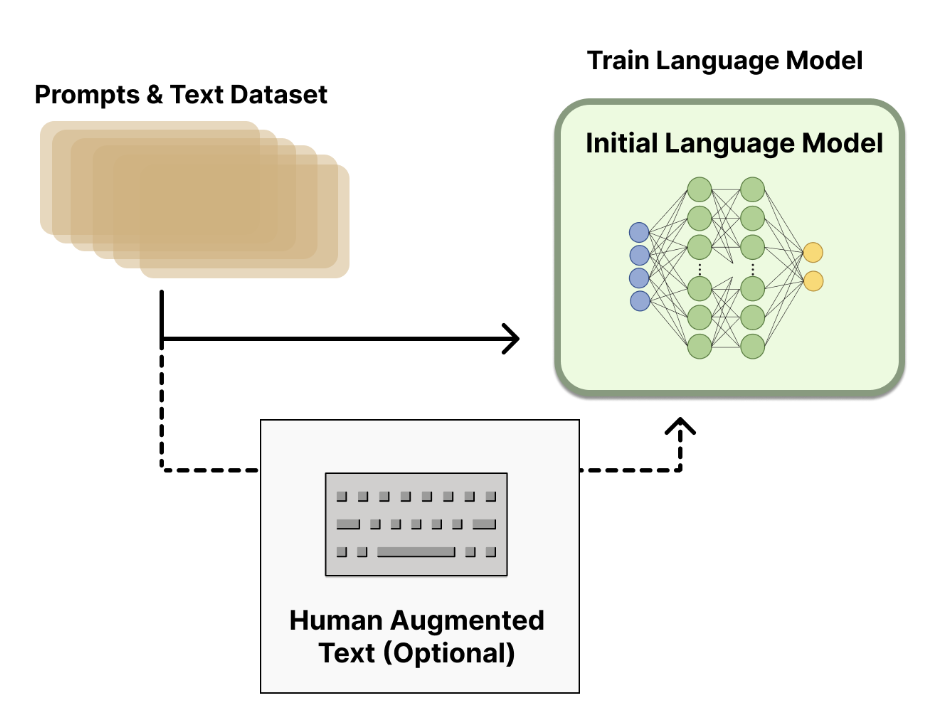
预训练模型训练
通常采用传统的
LLM Pretrain和SFT(可选),该过程产出 后续RLHF训练过程中的初始化模型。
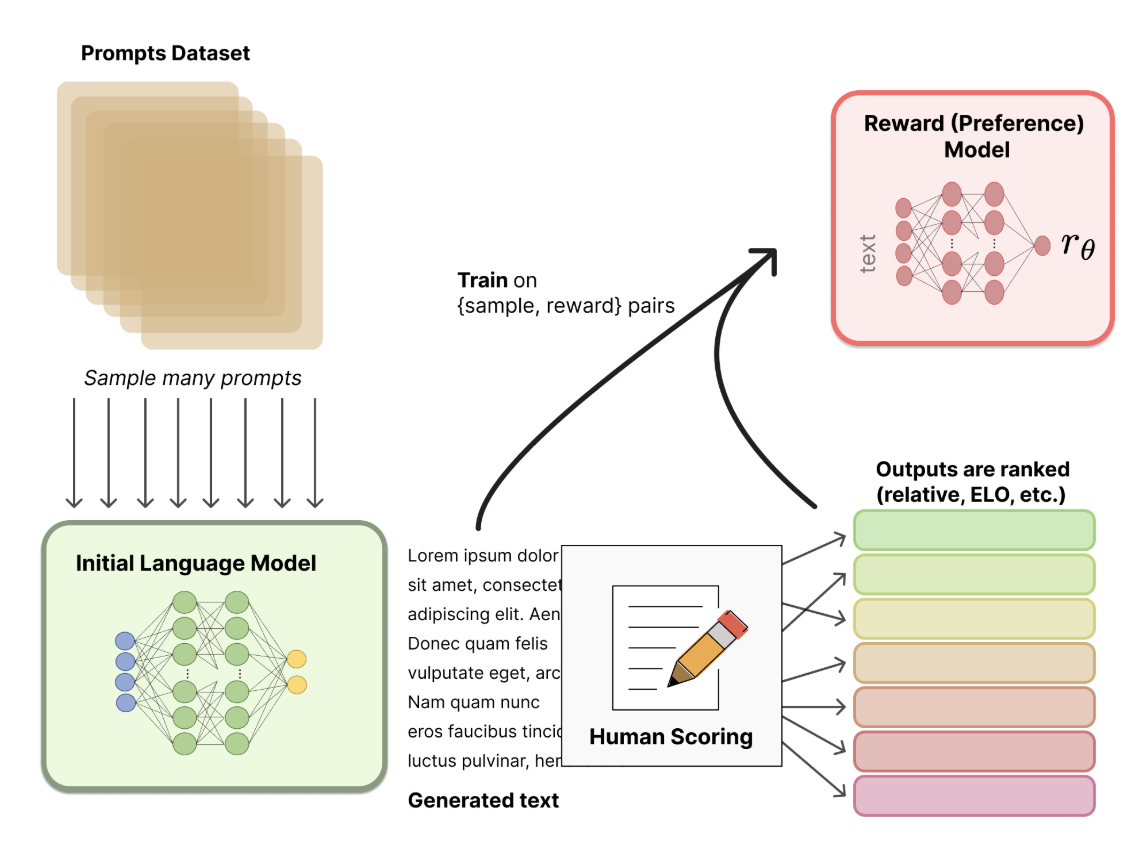
Reward Model训练
RM通常是经过微调的LLM,微调的数据来源人工标注得到。标注方式一般分为两种:
- 排序数据(
Pairwise Preference):标注员选择更好的输出,例如“输出 y_1 比 y_2 更优”。 - 绝对评分(Optional):为每个输出 y 分配一个分数,例如“输出 y_1 的评分为 4,y_2 的评分为 2”。
其中,绝对评分由于”标准难统一”、“个人价值观差异”通常噪声比较大。因此,通常采用排序的数据,奖励模型训练优化采用
pair wiss loss,即同时输入模型关于同一个问题的两个回答,让模型学会这两个句子哪个分高哪个分低。Reward Model结构上基于原始LLM模型扩展,通常通过添加一个线性回归头来实现:1 2 3 4 5 6 7
Pre-trained LM (Transformer) ↓ Pooling / Last Hidden State ↓ Linear Layer (Reward Head) ↓ Softmax: Scalar Reward Score R(y|x)
- 排序数据(
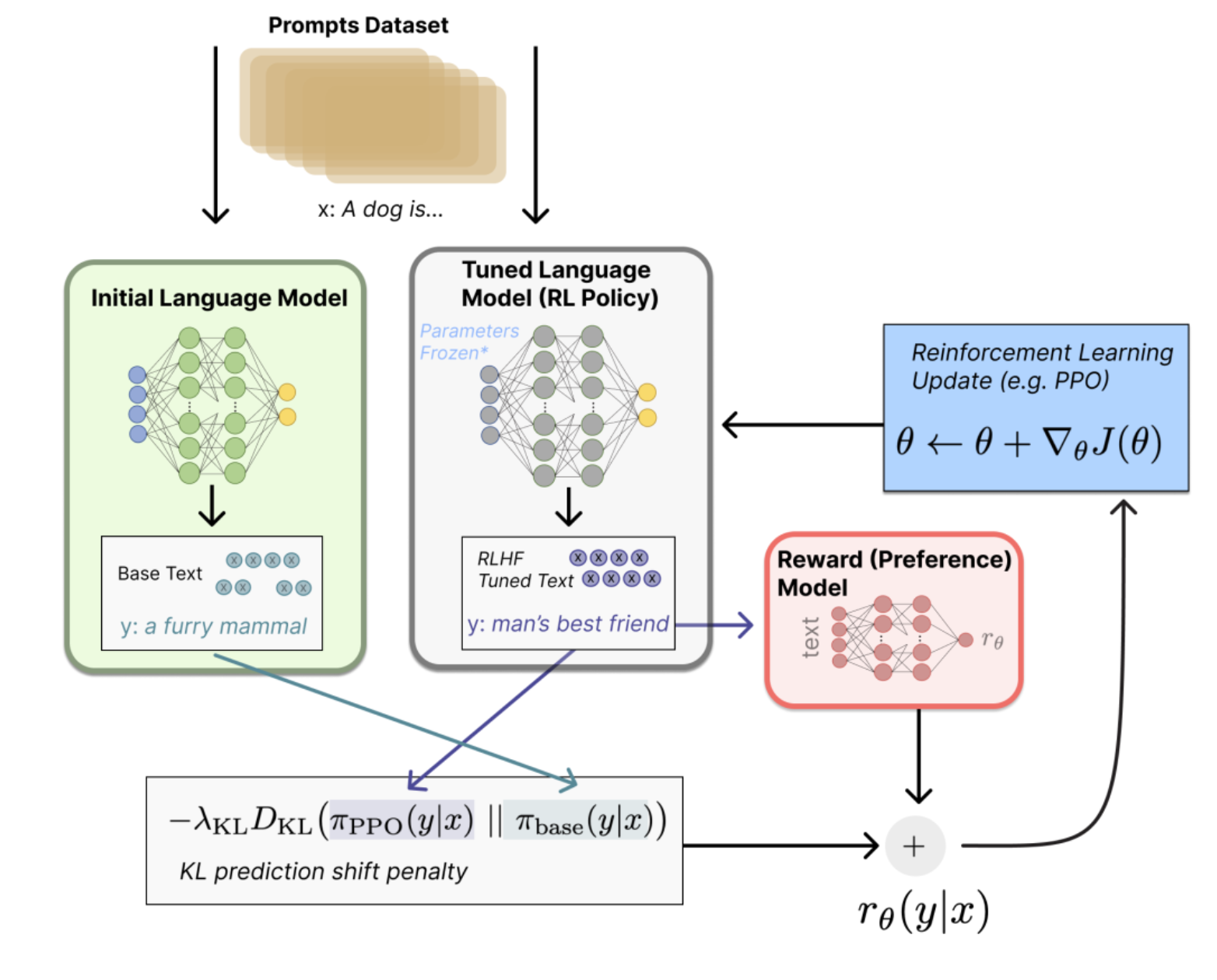
策略优化
在得到预训练Model/Reward Model后,便可以基于RL策略来进行模型的训练。将SFT任务转化为RL问题:策略的行动空间(
action space)是LM的原始所有词元,观察空间(observation space)是可能的输入词元序列,奖励函数是Reward Model和策略转变约束的结合。RL核心策略是近端策略优化(
Proximal Policy Optimization,PPO),其中的奖励函数为:初始LLM和微调LLM的输出文本的差异(比如KL散度),微调LLM的文本输入到RM得到的标量的reward。
RL算法
前文提到RL的算法的核心在于基于$s_t$来得到最佳的$a_t$的过程,其中$s_t$来源于状态空间,$a_t$来源于操作空间,而$s_t$到$a_t$来自于策略函数,$r_t$来源于奖励函数(包括惩罚项的负奖励)用于更新策略函数。核心步骤如下:
- 智能体观察环境状态$s_t$ 。
- 根据当前策略$\pi$ ,选择动作$a_t$ 。
- 环境接收动作$a_t$ ,返回奖励$r_t$和下一个状态$s_{t+1}$ 。
- 智能体基于奖励$r_t$ 和$s_{t+1}$ 学习和更新策略$\pi$ 。
- 重复以上过程,直到任务完成或达到终止条件。
策略学习的核心逻辑是基于价值函数(Value Function)引导智能体学习最优策略,价值函数通常可分为两类:
On-Policy Value Function
基于状态值$s$的价值函数$V^{\pi}(s)$
\[V^{\pi}(s) = \mathop{E}\limits_{\tau \sim \pi}[{R(\tau)\left| s_0 = s\right.}]\]其中,$\pi$为策略函数,$\tau$为对应的轨迹,为state/action的集合:
\[\tau = (s_0, a_0, s_1, a_1, ...).\]$R(\tau)$为对应$\tau$累计的
\[R(\tau) = \sum_{t=0}^{\infty} \gamma^t r_t.\] \[r_t = R(s_t, a_t, s_{t+1})\]Reward:On-Policy Action-Value Function
基于状态-动作的价值函数$Q^{\pi}(s,a)$
\[Q^{\pi}(s,a) = \mathop{E}\limits_{\tau \sim \pi}[{R(\tau)\left| s_0 = s, a_0 = a\right.}]\]
理想情况下,需要最大化价值函数:
\[Q^*(s,a) = \max_{\pi} \mathop{E}\limits_{\tau \sim \pi}{[R(\tau)\left| s_0 = s, a_0 = a\right.}]\] 如果已知$Q^*$,则可直接获取的到最优的$a^*(s)$:
\[a^*(s) = \arg \max_a Q^* (s,a)\]另外部分场景下,需要关注具体Action的相对优势($Advantage\ Function$):
\[A^{\pi}(s,a) = Q^{\pi}(s,a) - V^{\pi}(s)\]价值函数遵循Bellman equations,核心描述状态/状态-动作的价值递归关系:
The value of your starting point is the reward you expect to get from being there, plus the value of wherever you land next.
价值函数的Bellman equations为:
其中,$r$对应的当前的即时奖励,$ \gamma \in [0,1] $为折扣因子,控制短期和长期奖励的权衡,$P$描述的是$\tau$的生成概率,T-step下的策略轨迹可以表达为:
\[P(\tau|\pi) = \rho_0 (s_0) \prod_{t=0}^{T-1} P(s_{t+1} | s_t, a_t) \pi(a_t | s_t).\]意味着,每次的策略选择$a_t$都需要尽可能得到更高的$Q^\pi$。
整体过程实质是Markov Decision Process(MDPs),单个MDP为5元组, $\langle S, A, R, P, \rho_0 \rangle$其中:
- $S$对应所有的有效状态,
- $A$对应所有的动作,
- $R : S \times A \times S \to \mathbb{R} $对应
Reward Function,即:$r_t = R(s_t, a_t, s_{t+1})$, - $P:S \times A \to \mathcal{P}(S)$ :对应的是转换概率函数,其中 $P(s’|s,a)]$ 为基于$s$和$a$转换为$s’$的概率,
- $\rho_0$为初始状态分布。
PPO算法
PPO (``Proximal Policy Optimization)于2017年由OpenAI提出,其本身为基于TRPO算法的优化。两者都属于策略优化(Policy Optimization`)算法,一般包含两种算法:
Policy Gradient Methods
基于策略梯度优化目标函数,其中最常用的目标函数($Loss$)形式为:
Trust Region Methods
核心思路是通过限制心就策略之间的差异来控制策略更新的幅度,如
TRPO中的KL散度约束:
PPO算法在以上基础上,提出的核心优化思路为:
PPO-Clip
通过裁剪 $r_t(\theta)$ 的范围,避免更新过大,目标函数为:
\[L^\text{CLIP}(\theta) = \mathbb{E}_t \left[ \min \left( r_t(\theta) A_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) A_t \right) \right]\]其中:
- $r_t(\theta) = \frac{\pi_\theta(a_t | s_t)}{\pi_{\text{old}}(a_t | s_t)}$ 是概率比值。
- $ \epsilon$ 是裁剪范围(一般取 0.1 或 0.2)。
裁剪机制解释:
- 当$r_t(\theta) $偏离$ [1-\epsilon, 1+\epsilon] $时,将其限制在裁剪范围内,避免更新幅度过大。
- 保证优化过程中,新策略不会过分偏离旧策略,提升训练稳定性。
PPO-KL
将 KL 散度作为正则项添加到目标函数中,目标函数为:
\[L^\text{KL}(\theta) = \mathbb{E}t \left[ L^\text{PG}(\theta) - \beta {\text{KL}} \left[ \pi_{\text{old}}(\cdot | s_t),\pi_\theta(\cdot | s_t) \right] \right]\]其中:
- $D_{\text{KL}}$是新旧策略之间的 KL 散度。
- $\beta$是正则化系数,用于控制 KL 散度的影响,需要动态调整:
- $d=E_t\left[{\text{KL}} \left[ \pi_{\text{old}}(\cdot | s_t), \pi_\theta(\cdot | s_t) \right] \right]$
- $If\ d < d_{targ}/1.5, \beta \leftarrow \beta/2$
- $If\ d > d_{targ}/1.5, \beta \leftarrow \beta \times2$
PPO策略迭代还是基于策略梯度优化过程,每次迭代包括以下步骤:
Step 1: 采样
使用当前策略 $\pi_\theta$ 与环境交互,生成一批轨迹 $\tau$ :
\[\tau = \{(s_1, a_1, r_1), (s_2, a_2, r_2), \dots\}\]Step 2: 计算优势函数
通过以下公式计算优势函数 $A_t$ :
\[A_t = \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2} + \dots\]其中 $\delta_t$ 是时间步 t 的 TD 误差:
\[\delta_t = r_t + \gamma V_\phi(s_{t+1}) - V_\phi(s_t)\]Step 3: 策略更新
优化目标函数(PPO-Clip 或 PPO-KL)更新策略参数 $\theta$ :
\[\theta \leftarrow \arg\max_\theta L^\text{CLIP}(\theta) \quad \text{或} \quad L^\text{KL}(\theta)\]Step 4: 价值函数更新
优化均方误差(MSE)目标函数更新价值函数参数 $\phi$ :
\[L^\text{VF}(\phi) = \mathbb{E}t \left[ \left( V\phi(s_t) - \hat{R}_t \right)^2 \right]\]其中 $\hat{R}_t$ 是从轨迹采样估计的回报。
Step 5: 重复
重复采样和更新过程,直至达到收敛条件。
工程细节
这里以OpenRLHF实现为例,其实现上,训练框架基于DeepSpeed,模型库基于
HuggingFace,分布式扩展基于ray,推理框架添加了vLLM的加持,整体框架如下:
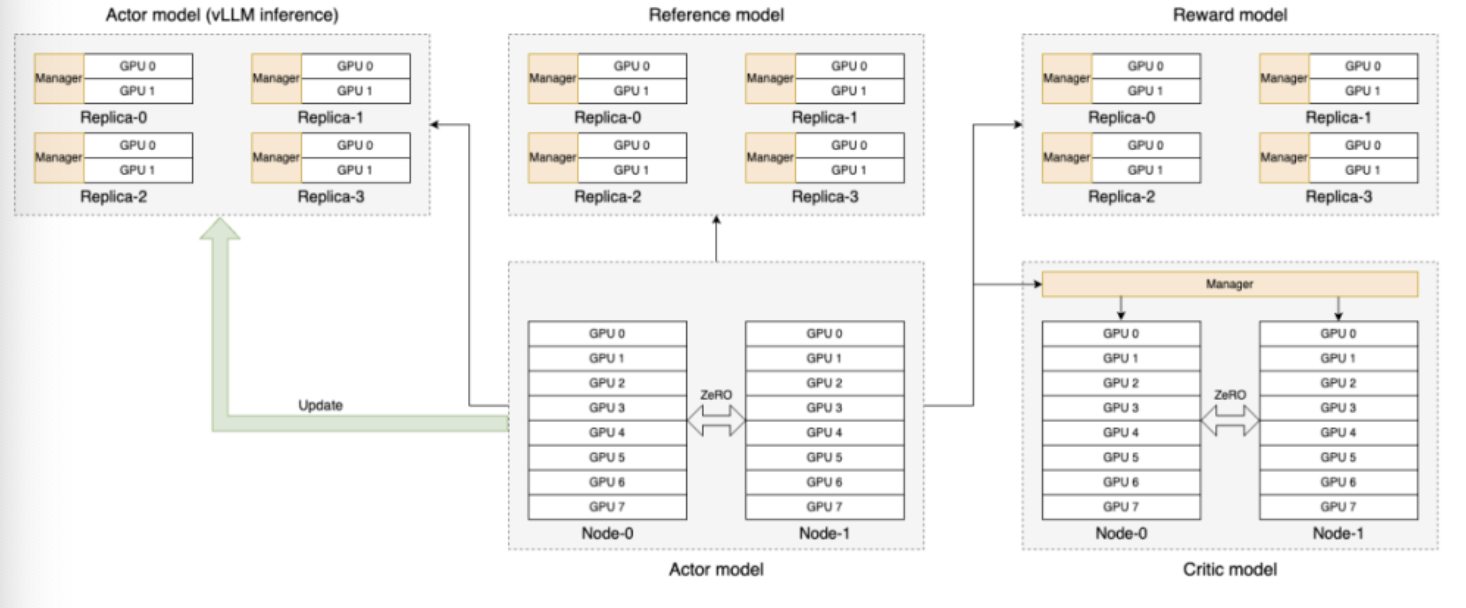
数据流如下: