前言
在大规模语言模型(LLMs, Large Language Models)中,由于 Transformer 模型本身不具备天然的序列感知能力,所以需要引入位置编码的目的是帮助模型捕捉和理解输入序列中位置关系和顺序信息。
绝对位置编码
绝对位置编码将每个位置直接编码为唯一的固定向量。常见的绝对位置编码包括:
可学习位置编码
每个位置对应一个可训练向量,由模型学习其语义,如可学习的
Posional Embedding。固定正弦-余弦位置编码(Sinusoidal PE)
\[\text{PE}{(pos, 2i)} = \sin(\frac {pos} {10000^{2i/d}})\] \[\text{PE}{(pos, 2i+1)} = \cos(\frac {pos} {10000^{2i/d}})\]Google在Attention Is All You Need提出,使用正弦和余弦函数生成位置向量,周期性和递减频率允许模型自然扩展到未见长度:
绝对位置编码的问题在于:
不具备外推的性质。因为绝对位置编码无法反应相对位置信息,因此对于模型输入长度超出训练阶段的模型最大长度时,模型效果会直线下降。Sinusoidal可以学到相对位置信息,且会存在远程衰减,但是其相对位置信息在$QK^T$内积之后无法反映。
RoPE
理想情况下,一个好的位置编码应该满足以下条件:
- 每个位置输出一个唯一的编码
- 具备良好的外推性:即$QK^T$内积之后仍然保有相对位置信息
- 任何位置之间的相对距离在不同长度的句子中应该是一致的
ROPE的推导过程如下:
假定$q/k/v$的计算函数为$f$,会基于词嵌入向量$x$计算$q/k/v$的同时引入位置编码:
\[q_m=f_q(x_m, m)\] \[k_n=f_k(x_n, n)\] \[v_n=f_v(x_n, n)\]其中,其中$m/n$表示位置信息。以$g$表示$q/k$的内积:
\[<f_q(x_m,m),f_k(x_n,n)>=g(x_m,x_n,m-n)\]$g$函数输入为相对位置$m-n$,即需要找到合适的位置编码来满足上述等式。可以引入欧拉公式:
\[e^{ix}=\text{cos}x+i\text{sin}x\]即:
\[f_q(x_m, m) = (W_qx_m)e^{imθ}\] \[f_k(x_n, n) = (W_kx_n)e^{inθ}\] \[g(x_m, x_n, m − n) = \text{Re}[(W_qx_m)(W_kx_n) ∗ e^{i(m−n)θ}]\]而对单独$f$按照邻近向量二维展开,可以看到:
\[q_m=\begin{pmatrix} q_m^{(1)} \\ q_m^{(2)}\end{pmatrix}=\begin{pmatrix} W_q^{(11)} & W_q^{(12)} \\ W_q^{(21)} &W_q^{(22)}\end{pmatrix}\begin{pmatrix} x_m^{(1)} \\ x_m^{(2)}\end{pmatrix}\]进一步表达为复数形式:
\[q_m=[q_m^{(1)},q_m^{2}]=q_m^{(1)}+iq_m^{(2)}\]可得:
\[q_me^{im\theta}=(q_m^{(1)}+iq_m^{(2)})*(\text{cos}(m\theta)+i\text{sin}(m\theta))=(q_m^{(1)}\text{cos}(m\theta)-q_m^{(2)}\text{sin}(m\theta))+i(q_m^{(2)}\text{cos}(m\theta)+q_m^{(1)}\text{sin}(m\theta))\]上述其实就是对应RoPE的旋转矩阵:
\[f_q(x_m,m)=\begin{pmatrix} \text{cos}m\theta & -\text{sin}m\theta \\ \text{sin}m\theta & \text{cos}m\theta\end{pmatrix}\begin{pmatrix} q_m^{(1)} \\ q_m^{(2)}\end{pmatrix}=R^d_{\Theta,m}\begin{pmatrix} q_m^{(1)} \\ q_m^{(2)}\end{pmatrix}\]将2维矩阵扩充到多维,旋转矩阵表示为:
\[R^d_{\Theta,m}=\begin{pmatrix} \text{cos}m\theta_0 & -\text{sin}m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\ \text{sin}m\theta_0 & \text{cos}m\theta_0 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \text{cos}m\theta_1 & -\text{sin}m\theta_1 & \cdots & 0 & 0 \\ 0 & 0 & \text{sin}m\theta_1 & \text{cos}m\theta_1 & \cdots & 0 & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \text{cos}m\theta_{d/2-1} & -\text{sin}m\theta_{d/2-1} \\ 0 & 0 & 0 & 0 & \cdots & \text{sin}m\theta_{d/2-1} & \text{cos}m\theta_{d/2-1}\end{pmatrix}\begin{pmatrix} q_m^{(1)} \\ q_m^{(2)}\end{pmatrix}\] \[\Theta=\{\theta_i=1000^{-2(i-1)/d},i\in[0,1,\cdots,d/2] \}\]由于$R^d_{\Theta,m}$的稀疏性,直接矩阵乘效率降低,可以采用下面实现:
\[R^d_{\Theta,m}x=\begin{pmatrix}x_0 \\ x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_{d-2} \\ x_{d-1}\end{pmatrix} \otimes \begin{pmatrix}\text{cos}m\theta_0 \\ \text{cos}m\theta_0 \\ \text{cos}m\theta_1 \\ \text{cos}m\theta_1 \\ \vdots \\ \text{cos}m\theta_{d/2-1} \\ \text{cos}m\theta_{d/2-1}\end{pmatrix}+\begin{pmatrix}-x_1 \\ x_0 \\ -x_3 \\ x_2 \\ \vdots \\ -x_{d-1} \\ x_{d-2}\end{pmatrix} \otimes \begin{pmatrix}\text{sin}m\theta_0 \\ \text{sin}m\theta_0 \\ \text{sin}m\theta_1 \\ \text{sin}m\theta_1 \\ \vdots \\ \text{sin}m\theta_{d/2-1} \\ \text{sin}m\theta_{d/2-1}\end{pmatrix}\]因此,RoPE的的计算过程如下:
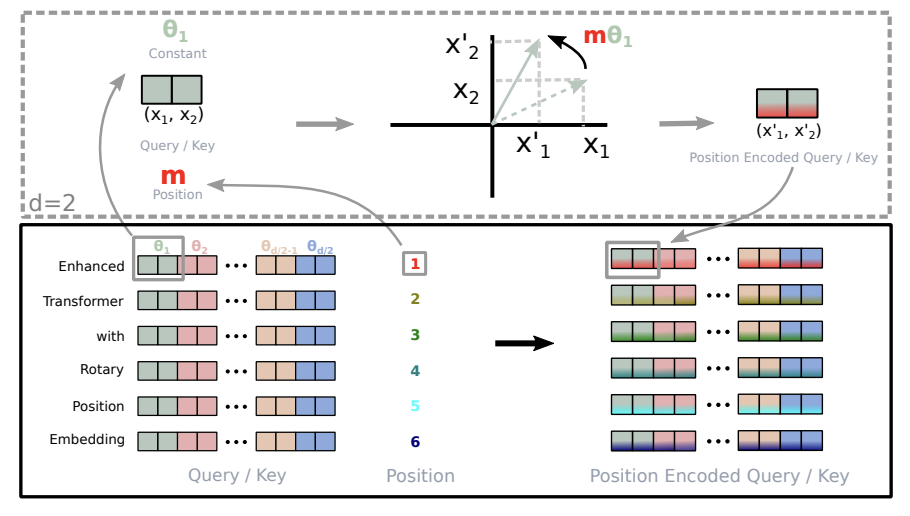
对于token序列的词嵌入向量,先计算query/key的向量,然后计算对应的旋转位置编码,然后对于query/key两两一组应用旋转变换,最后计算内积。
ALiBi
ALiBi(Attention with Linear Biases)发表于ICLR2022,机构包括。ALiBi的核心思路在于:
Attention with Linear Biases, biases query-key attention scores with a penalty that is proportional to their distance.
AliBi在$QK^T$的结果上直接填上一个与相对位置相关的线性的偏置:
其中,$b(i,j)$为线性偏置:
\[b(i,j)=-|i-j| \cdot m\]其中,$i,j$表示$query/key$的序列位置索引;$m$为缩放系数,本身是属于head-specific slope,对应$2^{\frac {-8} {n}}$,如对于8 heads,则$m=\frac{1}{2^1},\frac{1}{2^2},\cdots,\frac{1}{2^8}$。
