Posts Kaggle-Digit Recognizer-Dimensionality Reduction
Post
Cancel

Kaggle-Digit Recognizer-Dimensionality Reduction

Johney Zheng Jan 22, 2019 2019-01-22T22:56:24+08:00
Aug 21, 2021 2021-08-21T14:06:13+08:00 11 min

参考网页

动态图没法动态显示，动态显示效果可参考本人工程

Introduction:

  • Principal Component Analysis (PCA) –Unsupervised, liner method
  • Linear Discriminant Analysis (LDA) –Supervised, liner method
  • t-distributed Stochastic Neighbour Embedding (t-SNE) –Nonlinear, probabilstic method
1
2
3
4
5
6
7
8
9
10
11
12

import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)

import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import seaborn as sns
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import matplotlib
%matplotlib inline

1
2
3
4

# import the 3 dimensionality reduction methods
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

MNIST Dataset

1
2

train = pd.read_csv('../input/train.csv')
train.head()
labelpixel0pixel1pixel2pixel3pixel4pixel5pixel6pixel7pixel8...pixel774pixel775pixel776pixel777pixel778pixel779pixel780pixel781pixel782pixel783
01000000000...0000000000
10000000000...0000000000
21000000000...0000000000
34000000000...0000000000
40000000000...0000000000

5 rows × 785 columns

1

print(train.shape)

1

(42000, 785)

Pearson Correlation Plot(威尔逊相关系数)

1
2
3

# 先把标签数据从数据库中分离出来
target = train['label']
train = train.drop("label", axis=1)

1. PCA

Calculating the Eigenvectors

1
2
3
4

# Standardize the data
from sklearn.preprocessing import StandardScaler
X = train.values
X_std = StandardScaler().fit_transform(X)

1
2
3
4
5
6
7

/usr/local/lib/python3.5/dist-packages/sklearn/utils/validation.py:595: DataConversionWarning:

Data with input dtype int64 was converted to float64 by StandardScaler.

/usr/local/lib/python3.5/dist-packages/sklearn/utils/validation.py:595: DataConversionWarning:

Data with input dtype int64 was converted to float64 by StandardScaler.

1
2
3
4
5
6
7

# Calculating Eigenvectors and eigenvalues of Cov matrix
mean_vec = np.mean(X_std, axis=0)
cov_mat = np.cov(X_std.T)
eig_vals, eig_vecs = np.linalg.eig(cov_mat)
# Create a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i])
             for i in range(len(eig_vals))]

1
2
3
4
5
6
7
8

# Sort the eigenvalue, eigenvector pair from high to low
eig_pairs.sort(key=lambda x: x[0], reverse=True)
# Calculation of Explained Variance(可解释方差) from the eigenvalues
tot = sum(eig_vals)
# Individual explanined variance(个体可解释方差)
var_exp = [(i/tot)*100 for i in sorted(eig_vals, reverse=True)]
# (累积可解释方差)
cum_var_exp = np.cumsum(var_exp)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

# Use Plotly visualisation package
# To produce an interactive chart (互动图)
trace1 = go.Scatter(
    x = list(range(784)), # 28*28
    y = cum_var_exp,
    mode = 'lines+markers',
    name = "'Comulative Explained Variance'",
    # hoverinfo = cum_var_exp,
    line = dict(
        shape = 'spline',
        color = 'goldenrod'
    )
)
trace2 = go.Scatter(
    x = list(range(784)),
    y = var_exp,
    mode = 'lines+markers',
    name = "'Individual Explanined Variance'",
    # hoverinfo = cum_var_exp,
    line = dict(
        shape = 'linear',
        color = 'black'
    )
)
fig = tls.make_subplots(insets=[{'cell': (1,1), 'l':0.7, 'b':0.5}],print_grid=True)
fig.append_trace(trace1, 1, 1)
fig.append_trace(trace2, 1, 1)
fig.layout.title = 'Explained Variance plots - Full and Zoomed-in'
fig.layout.xaxis = dict(range=[0, 80], title='Feature columns')
fig.layout.yaxis = dict(range=[0, 60], title='Explained Variance')

py.iplot(fig, filename='inset example')

1
2
3
4
5
6
7

    This is the format of your plot grid:
    [ (1,1) x1,y1 ]

    With insets:
    [ x2,y2 ] over [ (1,1) x1,y1 ]

图片1

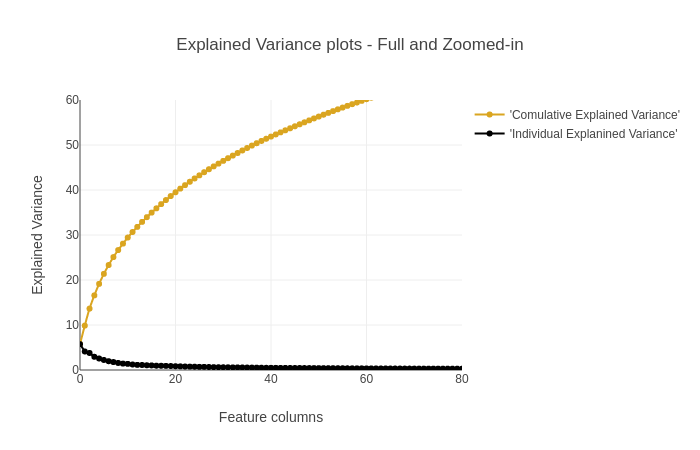
上图累计解释方差图可知874个数据，利用其中的200个数据便构成了90%的累积方差。所以在特征降维的过程中，只提取得到该200个特征便可以一定程度上替代整个样本。

Visualizing the Eigenvalues

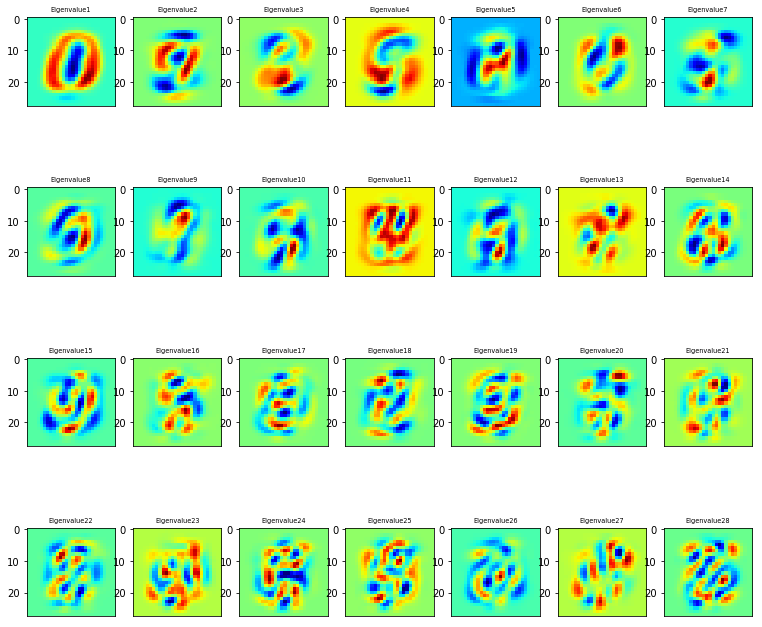
采用了sklearn从dataset中提取30 eigenvalues，并且可视化比较最高的28个eigenvalues

1
2
3
4
5
6
7
8

# Invoke Sklearn's PCA method
n_components = 30
pca = PCA(n_components=n_components).fit(train.values)

eigenvalues = pca.components_.reshape(n_components, 28, 28)

# Extract the PCA components (eigenvalues)
eigenvalues = pca.components_

1
2
3
4
5
6
7
8
9
10
11
12
13
14

n_rows = 4
n_col = 7

# Plot the first 28 eigenvalues
plt.figure(figsize=(13,12))
for i in list(range(n_rows * n_col)):
    offset = 0
    plt.subplot(n_rows, n_col, i+1)
    plt.imshow(eigenvalues[i].reshape(28, 28), cmap='jet')
    title_text = 'Eigenvalue' + str(i+1)
    plt.title(title_text, size=6.5)
    plt.xticks(())
    plt.xticks(())
plt.show()

图片2

从上图可知，特征图的方向演变越来越复杂，以拓展特征空间，扩大特征方差。

Visualsing the MNIST Digit set on its own

展示实际基础数据集数据

1
2
3
4
5
6
7
8
9
10

# plot some of the numbers
plt.figure(figsize=(14, 12))
for digit_num in range(0, 70):
    plt.subplot(7, 10, digit_num+1)
    # reshape from 1d to 2d pixel array
    grid_data = train.iloc[digit_num].as_matrix().reshape(28, 28)
    plt.imshow(grid_data, interpolation="none", cmap='afmhot')
    plt.xticks([])
    plt.yticks([])
plt.tight_layout()

1
2
3

/usr/local/lib/python3.5/dist-packages/ipykernel_launcher.py:6: FutureWarning:

Method .as_matrix will be removed in a future version. Use .values instead.

图片3

PCA Implementation via Sklearn

PCA聚类的关键在于如何选取聚类的components，具体可参考论文，这里选取为5

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# Delete our earlier created X object
del X
# Taking only the first N rows to speed things up
X = train[:6000].values
del train
# Standardsing the values
X_std = StandardScaler().fit_transform(X)

# Call the PCA method with 5 components.
pca = PCA(n_components=5)
pca.fit(X_std)
X_5d = pca.transform(X_std)

# For cluster coloring in our Plotly plots, remember to also restrict the target values
Target = target[:6000]

1
2
3
4
5
6
7

/usr/local/lib/python3.5/dist-packages/sklearn/utils/validation.py:595: DataConversionWarning:

Data with input dtype int64 was converted to float64 by StandardScaler.

/usr/local/lib/python3.5/dist-packages/sklearn/utils/validation.py:595: DataConversionWarning:

Data with input dtype int64 was converted to float64 by StandardScaler.

Interactive visualisations of PCA representation

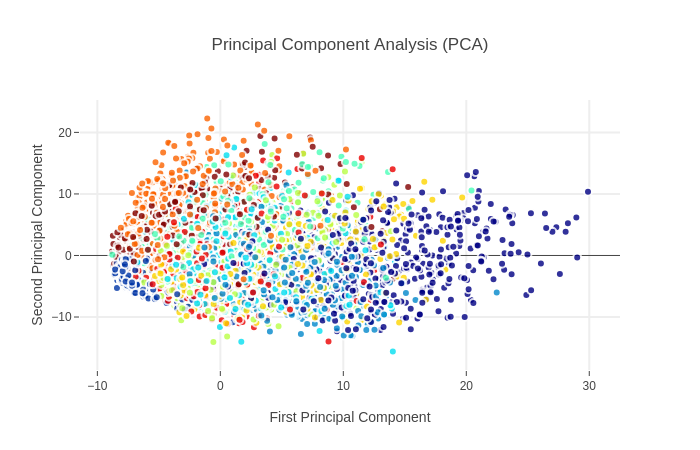
这里只显示前两主成分投影

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

trace0 = go.Scatter(
    x = X_5d[:, 0],
    y = X_5d[:, 1],
    mode = 'markers',
    text = Target,
    showlegend = False,
    marker = dict(
        size = 8,
        color = Target,
        colorscale = 'Jet',
        showscale = False,
        line = dict(
            width = 2,
            color = 'rgb(255, 255, 255)'
        ),
        opacity = 0.8
    )
)
data = [trace0]

layout = go.Layout(
    title = 'Principal Component Analysis (PCA)',
    hovermode = 'closest',
    xaxis = dict(
        title = 'First Principal Component',
        ticklen = 5,
        zeroline = False,
        gridwidth = 2,
    ),
    yaxis = dict(
        title = 'Second Principal Component',
        ticklen = 5,
        gridwidth = 2,
    ),
    showlegend = True,
)

fig = dict(data=data, layout=layout)
py.iplot(fig, filename='styled-scatter')

图片4

PCA属于非监督学习，类别信息是外加的，可以看到类别的分类情况不是特别好

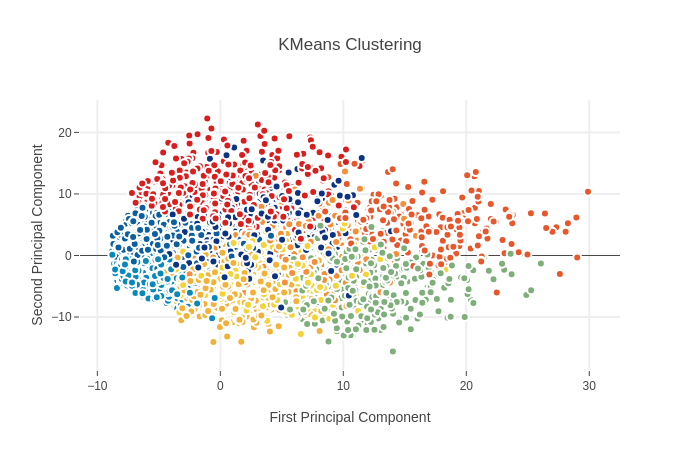
K-Means Clustering to identify possible classes

K-Means可用于PCA非监督学习中的聚类分析，通过点云集中心之间的距离来进行分类 这里显示前两主成分投影的聚类分析结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

from sklearn.cluster import KMeans # KMeans clustering
# KMeans 中K设置为9
kmeans = KMeans(n_clusters=9)
# Compute cluster centers and predict cluster indices
X_clustered = kmeans.fit_predict(X_5d)

trace_Kmeans = go.Scatter(x=X_5d[:, 0], y=X_5d[:, 1], mode="markers",
                         showlegend=False,
                         marker=dict(
                             size = 8,
                             color = X_clustered,
                             colorscale = 'Portland',
                             showscale = False,
                             line = dict(
                                 width = 2,
                                 color = 'rgb(255, 255, 255)'
                             )
                         ))

layout = go.Layout(
    title = 'KMeans Clustering',
    hovermode = 'closest',
    xaxis = dict(
        title = 'First Principal Component',
        ticklen = 5,
        zeroline = False,
        gridwidth = 2,
    ),
    yaxis = dict(
        title = 'Second Principal Component',
        ticklen = 5,
        gridwidth = 2,
    ),
    showlegend = True
)

data = [trace_Kmeans]
fig1 = dict(data=data, layout = layout)
py.iplot(fig1, filename='svm')

图片5

和之前PCA的图相比较可见非监督学习的分类效果不是很好，两者一致性较低

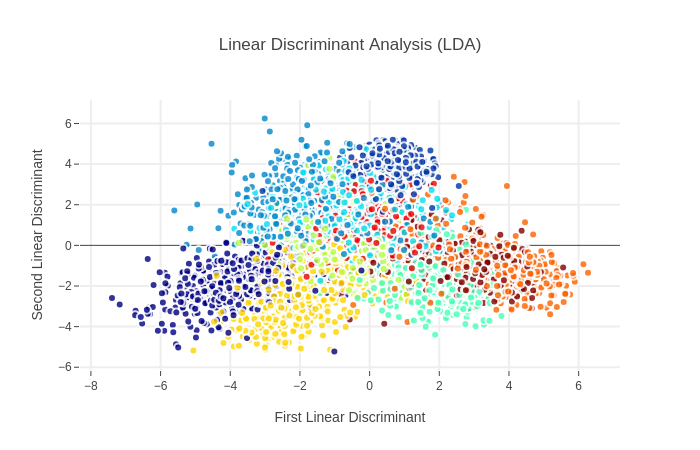
2. Linear Discriminant Analysis (LDA)

LDA的原理在于最大化类间方差，最小化类内方差，可通过散度矩阵进行表达求解

LDA Implementation via Sklearn

LDA model，仍采用5维度

1
2
3

lda = LDA(n_components=5)
# Taking in as second argument the Target as labels
X_LDA_2D = lda.fit_transform(X_std, Target.values)

1
2
3

/usr/local/lib/python3.5/dist-packages/sklearn/discriminant_analysis.py:388: UserWarning:

Variables are collinear.

Interactive visualisations of LDA representation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# Using the Plotly library again
traceLDA = go.Scatter(
    x = X_LDA_2D[:, 0],
    y = X_LDA_2D[:, 1],
    mode = 'markers',
    text = Target,
    showlegend = True,
    marker = dict(
        size = 8,
        color = Target,
        colorscale = 'Jet',
        line = dict(
            width = 2,
            color = 'rgb(255, 255, 255)'
        ),
        opacity = 0.8
    )
)
data = [traceLDA]

layout = go.Layout(
    title = 'Linear Discriminant Analysis (LDA)',
    hovermode = 'closest',
    xaxis = dict(
        title = 'First Linear Discriminant',
        ticklen = 5,
        zeroline = False,
        gridwidth = 2,
    ),
    yaxis = dict(
        title = 'Second Linear Discriminant',
        ticklen = 5,
        gridwidth = 2,
    ),
    showlegend = False
)

fig = dict(data=data, layout=layout)
py.iplot(fig, filename='styled-scatter')

图片6

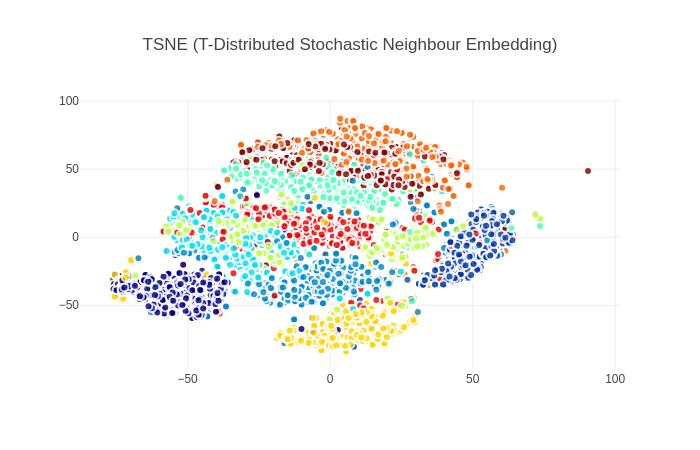
3. T-SNE(t-Distributed Stochastic Neighbour Embedding)

t分布以条件分布来解决分类问题

1
2
3

# Invoking the t-SNE method
tsne = TSNE(n_components=2)
tsne_results = tsne.fit_transform(X_std)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

traceTSNE = go.Scatter(
    x = tsne_results[:, 0],
    y = tsne_results[:, 1],
#    name = Target,
#    hoveron = Target,
    mode = 'markers',
    text = Target,
    showlegend = True,
    marker = dict(
        size = 8,
        color = Target,
        colorscale = 'Jet',
        showscale = False,
        line = dict(
            width = 2,
            color = 'rgb(255, 255, 255)'
        ),
        opacity = 0.8
    )
)
data = [traceTSNE]

layout = dict(title = 'TSNE (T-Distributed Stochastic Neighbour Embedding)',
             hovermode = 'closest',
             yaxis = dict(zeroline = False),
             xaxis = dict(zeroline = False),
             showlegend = False,
             )

fig = dict(data=data, layout=layout)
py.iplot(fig, filename='styled-scatter')

图片7

从图中可以看出TSNE算法的类间分离效果较好，优于之前的PCA和LDA算法，这要归结于算法的拓扑保留特性 TSNE算法的缺点在于可能存在多个局部最小值，图中可看出有相同颜色的子簇被分离到了两块不同的区域

4.总结

这里简单总结了几种常见的降维方法，包括：PCA（+KMeans），LDA，TSNE 还有一些其他的降维方案，包括：Sammon映射、多维缩放、以及一些基于图的可视化方法

Tutorial
Kaggle CV
This post is licensed under CC BY 4.0 by the author.
最近更新
文章目录

Kaggle-Digit Recognizer-MLP

Org-mode基本功能