GEMM算子优化
GEMM优化的核心在于:
- 提高Cache命中率,设计更好的数据排布(Tiling)
- 提高并行度,充分利用指令向量化和多核并行
先看一个native的实现:
1
2
3
4
5
6
7
8
9
10
void naive_row_major_sgemm(const float* A, const float* B, float* C, const int M,
const int N, const int K) {
for (int m = 0; m < M; ++m) {
for (int n = 0; n < N; ++n) {
for (int k = 0; k < K; ++k) {
C[m * N + n] += A[m * K + k] * B[k * N + n];
}
}
}
}
其浮点运算量为2xMxNxK,缓存读次数为2xMxNxK,写次数为MxN;但是这种写法会造成大量的Cache miss: 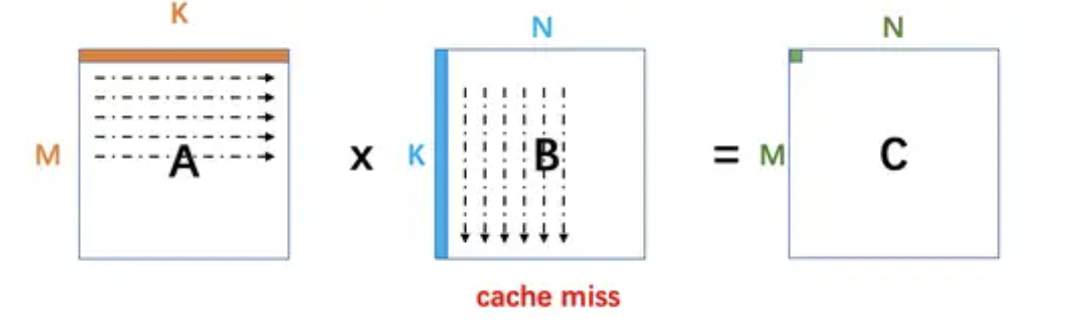
简单的循环重排就可以得到加速:
1
2
3
4
5
6
7
8
9
10
void optimize_row_major_sgemm(const float* A, const float* B, float* C, const int M,
const int N, const int K) {
for (int m = 0; m < M; ++m) {
for (int k = 0; k < K; ++k) {
for (int n = 0; n < N; ++n) {
C[m * N + n] += A[m * K + k] * B[k * N + n];
}
}
}
}
进一步提高性能,需要做矩阵A/B的分块计算,以CUDA而言:需要设计从Global Memory->Shared Memory->Register的分块逻辑,核心是提高Cache命中率。

引入共享内存缓存子矩阵块,可以减少对全局内存的访问:
- 每个线程块负责计算 C 的一个子矩阵块。
- 每次从全局内存加载一个子块到共享内存。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#define TILE_M 16
#define TILE_N 16
#define TILE_K 16
__global__ void gemm_tiled(float *A, float *B, float *C, int M, int N, int K) {
// 定义共享内存
__shared__ float tile_A[TILE_M][TILE_K];
__shared__ float tile_B[TILE_K][TILE_N];
// 计算当前线程块的位置
int block_row = blockIdx.y;
int block_col = blockIdx.x;
// 计算当前线程的位置
int thread_row = threadIdx.y;
int thread_col = threadIdx.x;
// 结果存储到寄存器
float value = 0.0f;
// 遍历所有子块
for (int k = 0; k < (K + TILE_K - 1) / TILE_K; ++k) {
// 加载 A 的子块到共享内存
if (block_row * TILE_M + thread_row < M && k * TILE_K + thread_col < K) {
tile_A[thread_row][thread_col] = A[(block_row * TILE_M + thread_row) * K + (k * TILE_K + thread_col)];
} else {
tile_A[thread_row][thread_col] = 0.0f;
}
// 加载 B 的子块到共享内存
if (k * TILE_K + thread_row < K && block_col * TILE_N + thread_col < N) {
tile_B[thread_row][thread_col] = B[(k * TILE_K + thread_row) * N + (block_col * TILE_N + thread_col)];
} else {
tile_B[thread_row][thread_col] = 0.0f;
}
__syncthreads();
// 从共享内存加载到寄存器并计算
for (int t = 0; t < TILE_K; ++t) {
value += tile_A[thread_row][t] * tile_B[t][thread_col];
}
__syncthreads();
}
// 写回全局内存
if (block_row * TILE_M + thread_row < M && block_col * TILE_N + thread_col < N) {
C[(block_row * TILE_M + thread_row) * N + (block_col * TILE_N + thread_col)] = value;
}
}
另外,为了减少循环控制的开销可以手动展开循环提升性能:假设矩阵维度是循环展开大小的倍数,将循环迭代分为固定大小的展开步长。
1
2
3
4
5
6
7
8
9
10
11
#define UNROLL_FACTOR 4 // 展开因子
// 原始实现:从共享内存加载到寄存器并计算
// for (int t = 0; t < TILE_K; ++t) {
// value += tile_A[thread_row][t] * tile_B[t][thread_col];
// }
for (int t = 0; t < TILE_K; t += UNROLL_FACTOR) {
value += tile_A[thread_row][t] * tile_B[t][thread_col];
value += tile_A[thread_row][t + 1] * tile_B[t + 1][thread_col];
value += tile_A[thread_row][t + 2] * tile_B[t + 2][thread_col];
value += tile_A[thread_row][t + 3] * tile_B[t + 3][thread_col];
}