Posts 2D_Detection-基本深度学习单元
Post
Cancel

2D_Detection-基本深度学习单元

Johney Zheng Aug 6, 2021 2021-08-06T22:25:12+08:00
Aug 21, 2021 2021-08-21T14:06:13+08:00
17 min

前言

深度学习目前在CV（Computer Vision）各个领域都有惊人的进展，从而也衍生了多样的深度学习网络结构；但是诸多复杂的网络结构仍然是基于诸多基础机构组成的，一些定制化的结构也可以认为是基础结构的变种。下文简单介绍几种基本的深度学习在CV领域的结构：

  • 卷积层
  • 激活函数
  • 池化层
  • BN层
  • Dropout层
  • 全连接层

卷积层

卷积操作类似滤波操作,原始图像可以通过卷积操作提取到图像的特征(如canny边缘特征等),不同的卷积核提取的特征不一致,CV的核心是通过可学习的卷积核层层提取特征,然后基于高维特征进行具体的任务.

传统卷积

卷积层通常指2D卷积层,其他还包括1D卷积层(通常处理如单维度的时序数据),3D卷积(常应用于视频处理和3D数据处理,3D卷积通常计算量很大且较为耗时). 2D卷积示意图: 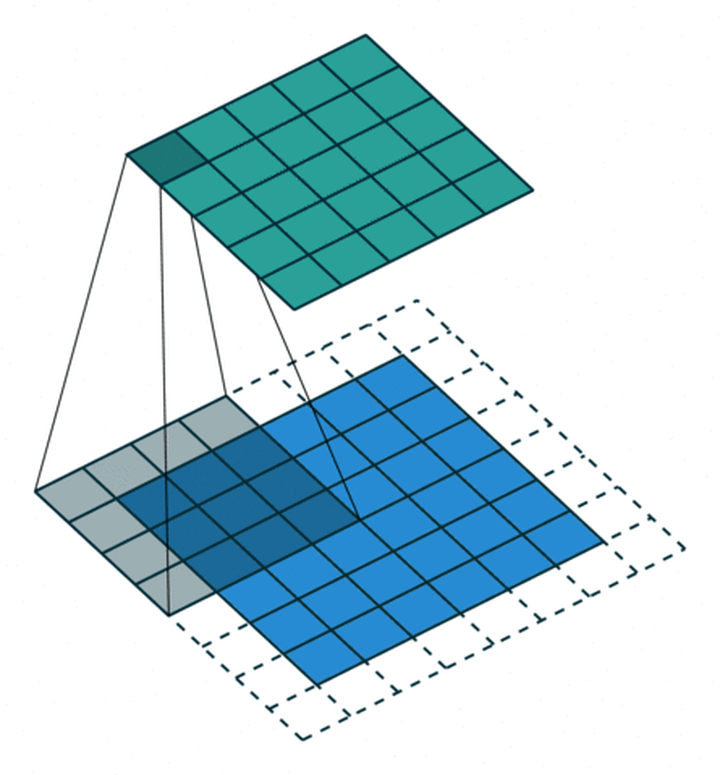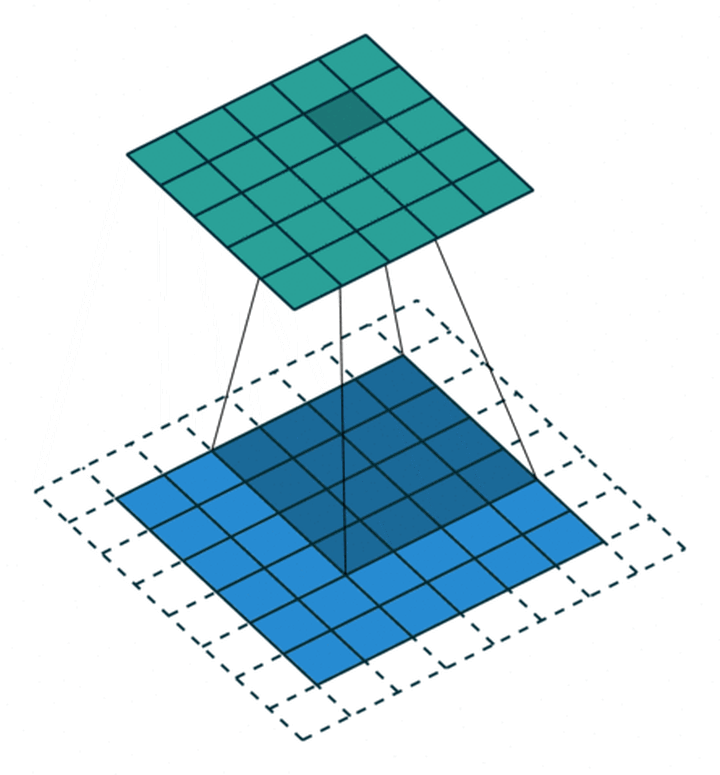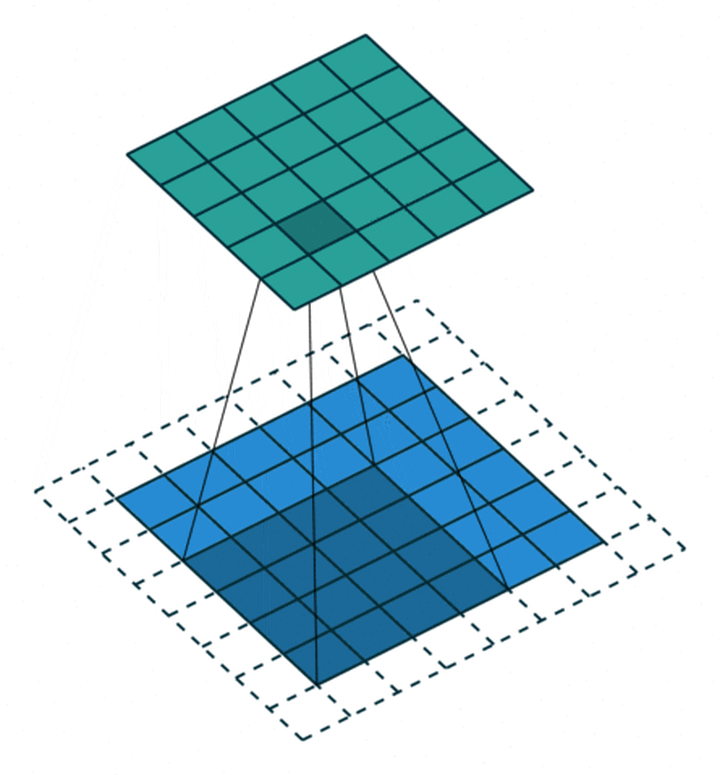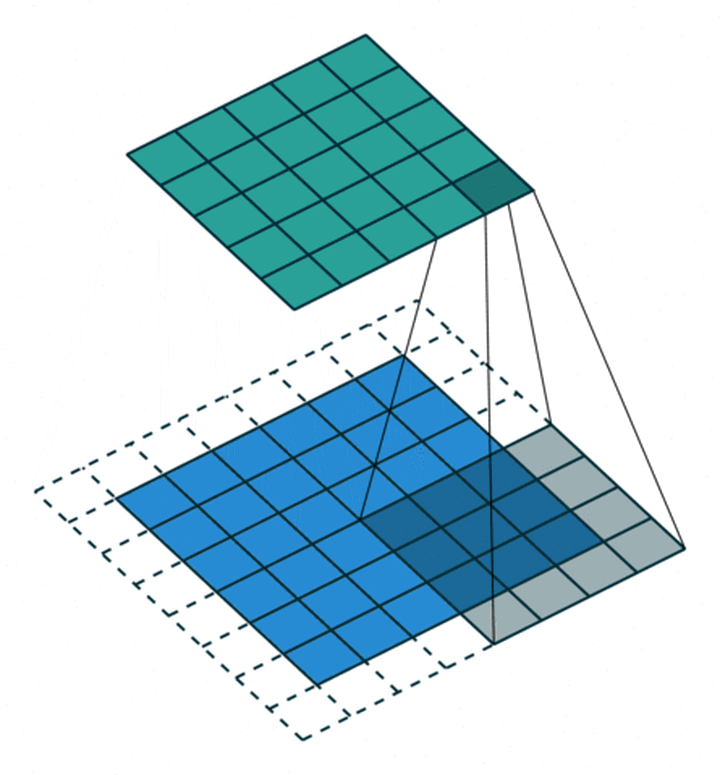img

3D卷积示意图: 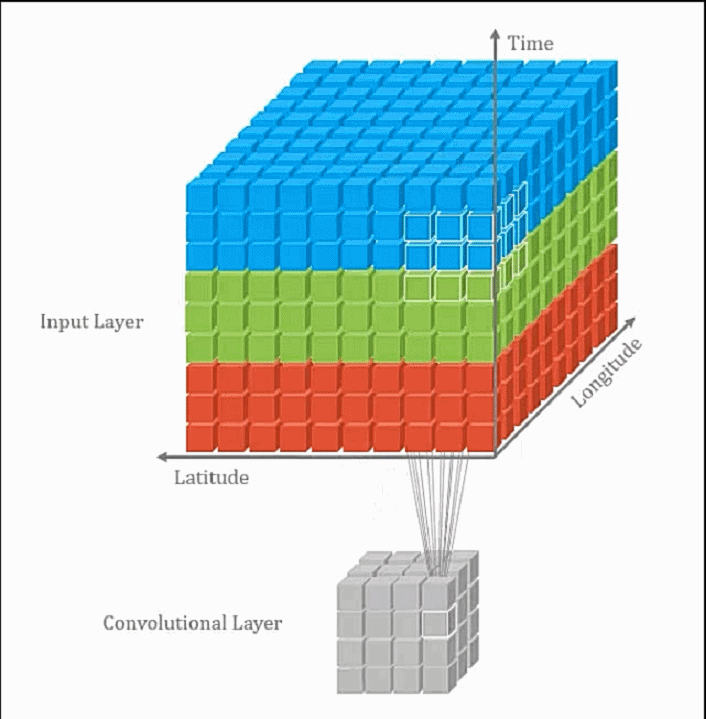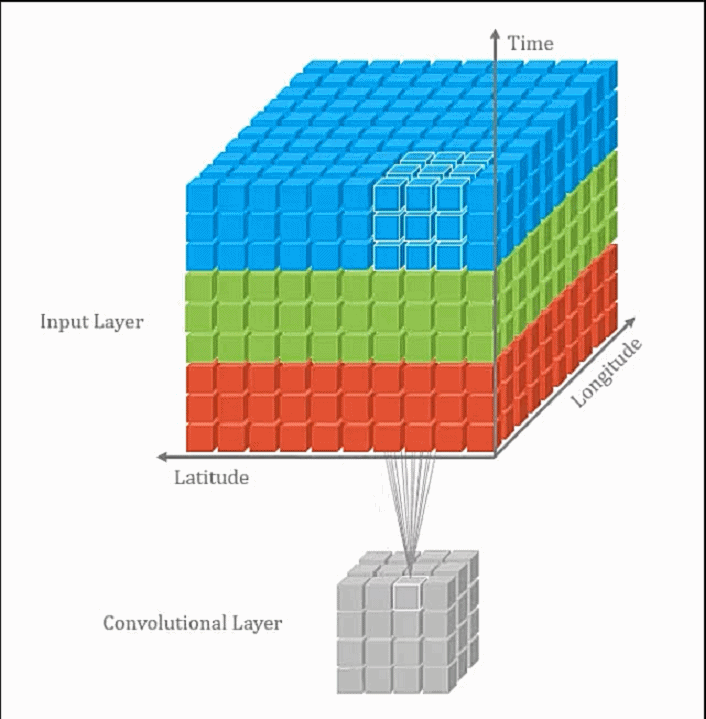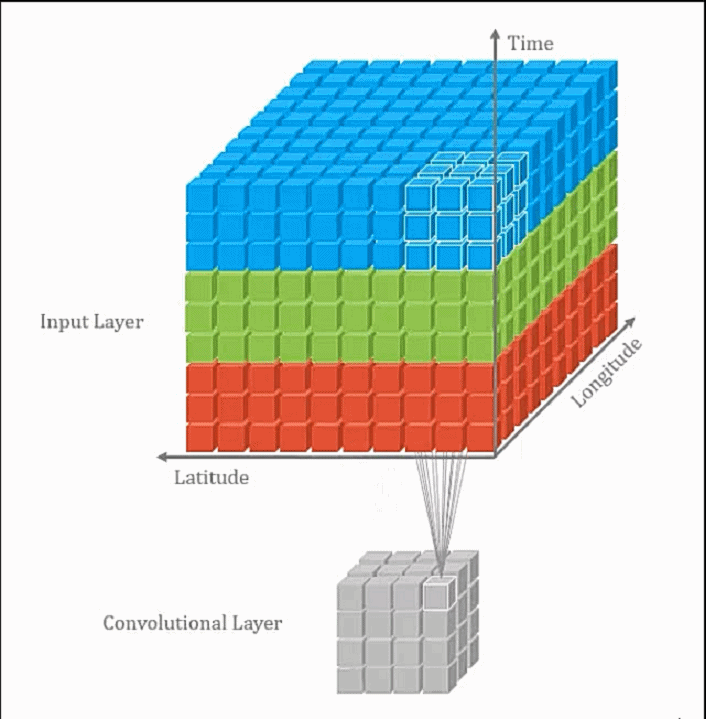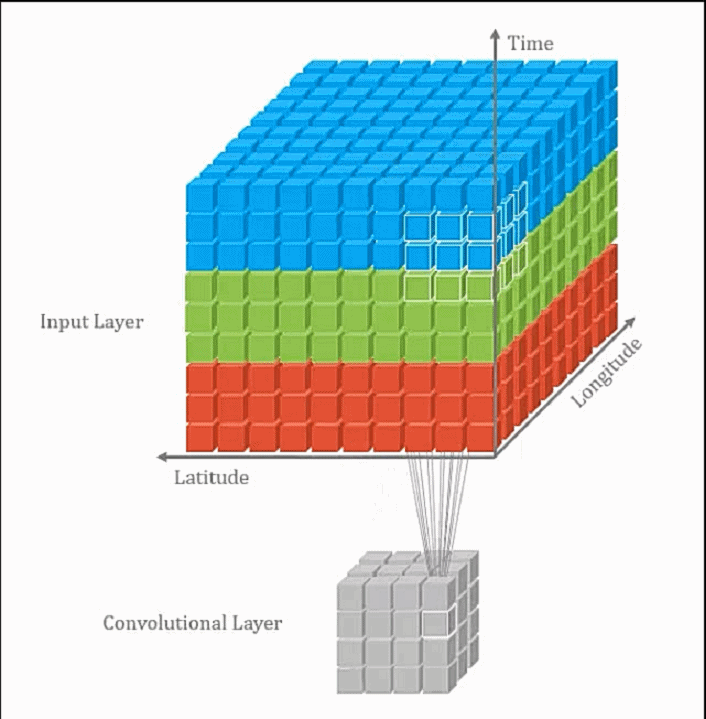img

padding 方式:进行卷积操作的时候,通常会进行padding操作,常见包括两种padding方式:

  • valid: 不进行padding操作,丢弃右侧(下侧)的列(行)

    valid: 方式的输出shape计算方式:

    \[W_{out} = ceil(\frac{W_{in} - K_w + 1}{S_w})\] \[H_{out} = ceil(\frac{H_{in} - K_h + 1}{S_h})\]

  • same: 尽可能均匀的进行上下左右padding,但是如果要添加的列/行的数量是奇数的话,same的方式会将额外的列添加到右/下列,添加行/列的计算通过保证前后输出shape的一致计算

    \[W_{out} = ceil(\frac{W_{in}}{S_w})\] \[H_{out} = ceil(\frac{H_{in}}{S_h})\]

可分离卷积

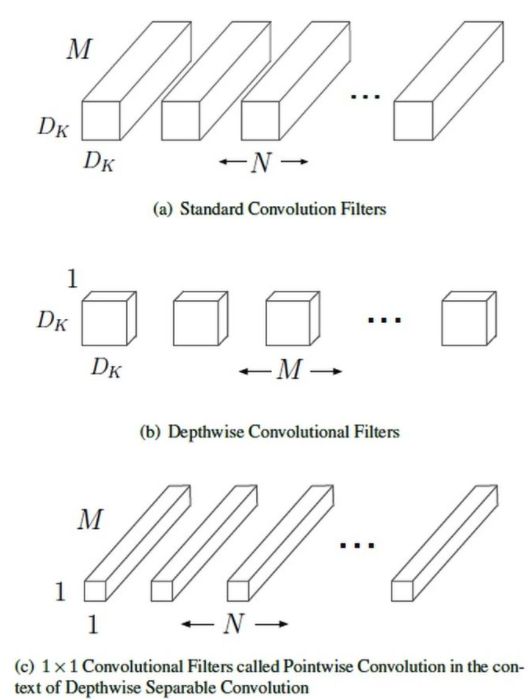
可分离卷积最早提出于mobilenet ,其核心在于将传统的卷积分为两个部分:深度卷积(depthwise convolution)和一个1X1的点卷积(pointwise convolution).

假设卷积的输入featuremap大小为 $D_F*D_F$​​​ ,输出特征图大小为 $D_F*D_F*N$​​​,卷积核为 $D_K$​​​,对于标准卷积,参数量为 $D_K*D_K*N*M$​​​,计算量为 $D_K*D_K*M*N*D_F*D_F$​​​.

深度卷积的卷积方式是先对输入特征的每个channel采用单独的 $D_K*D_K*1$的卷积操作,然后将concat形成 $D_F*D_F*M$的特征图,在使用N个$1*1*M$的卷积核进行卷积操作得到最终的 $D_F*D_F*N$ 的特征图输出,则其参数量为 $D_K*D_K*M+N*1*1*M$ ,计算量为 $D_K*D_K*M*D_F*D_F+1*1*M*D_F*D_F*N$ ,参数量和计算量的前后比值为 $1/N+1/(D_K*D_K)$ ,如卷积核大小为3,则比值接近1/9

深度卷积示意图:

img

另外Depthwise Convolution其实可以认为是Group Convolution的一种特例.

Group Convolution将输入的feature map分为G组,分组卷积(假设总输出Channel数为C,则每组的输出Channel为C/G):

此时假设featuremap数量为N,尺寸为 $H*W$ ,则卷积核尺寸为 $C/G*K*K$,卷积核的总参数为 $\frac{N*C}{G*K*K}$ (为原始卷积参数的$\frac{1}{G}$).当$G=N=C$,则Group Convolution等价于Depthwise Convolution.

转置卷积(反卷积)

转置卷积(反卷积)的作用在于将低分辨(小尺寸)到高分辨(大尺寸)特征图,上采样一般有两种方式:

  • 直接resize
  • 转置卷积

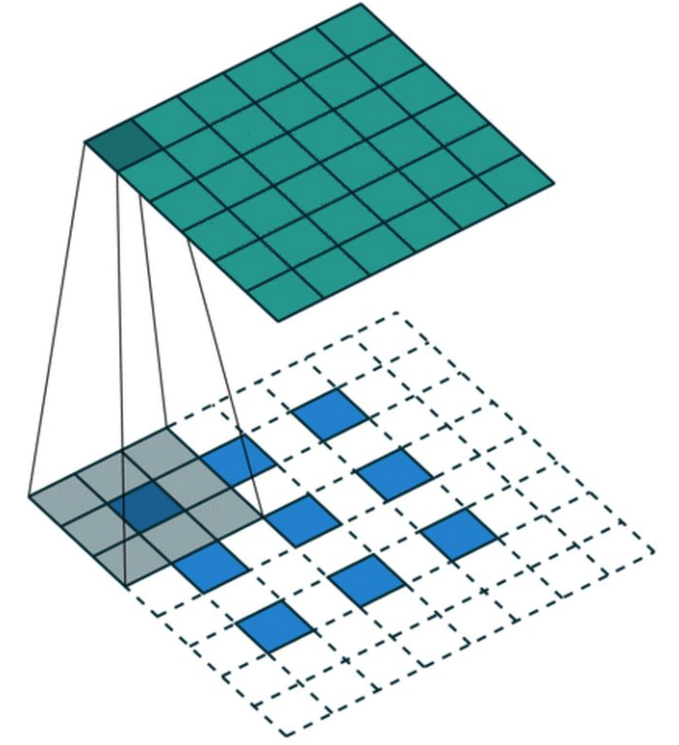
转置卷积可以认为卷积的反向操作,步长为1的卷积操作,一般步骤为:

  • 对输入进行padding操作
  • 进行卷积操作

正常卷积操作示例:

img

stride非1的转置卷积,则需要在feature map之间进行insert 0:

img

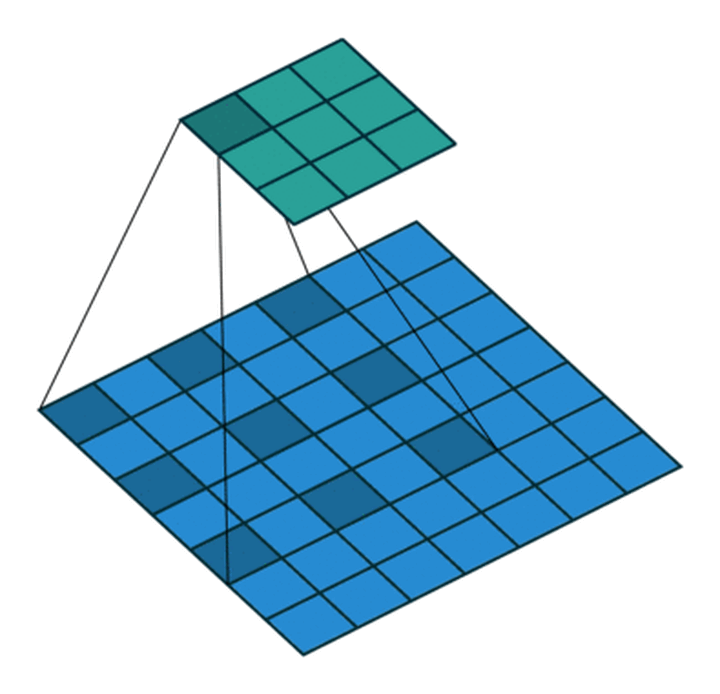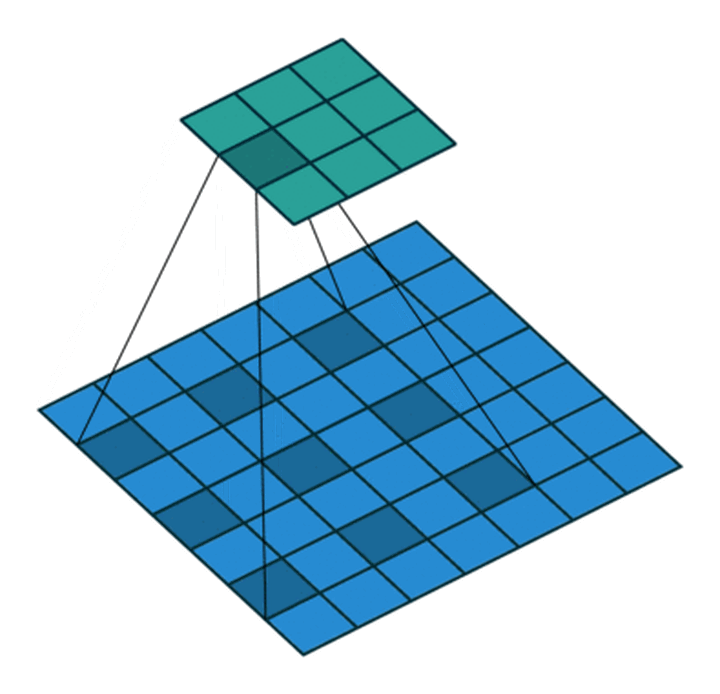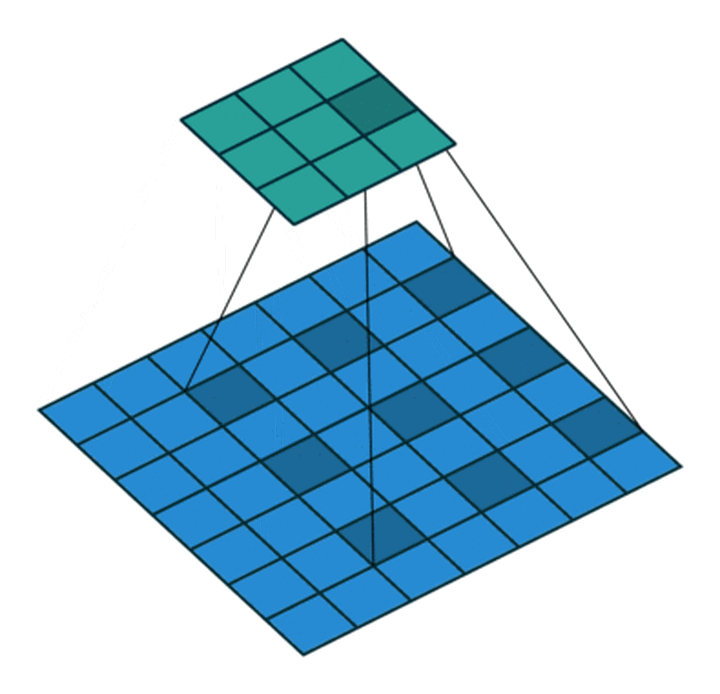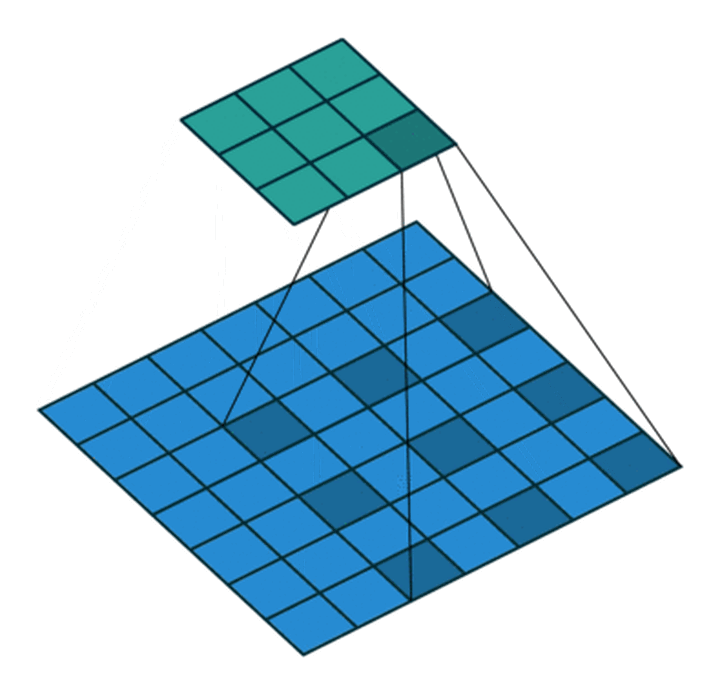
空洞卷积

空洞卷积能够在不改变参数的情况下增大卷积核的感受野,可以用于捕获多尺度信息. 空洞卷积一般有两种实现方式:

  • 卷积核填充0
  • 输入等间隔采样

其中,空洞卷积的卷积核间隔数量被称为膨胀率(diation rate).

img

可形变卷积

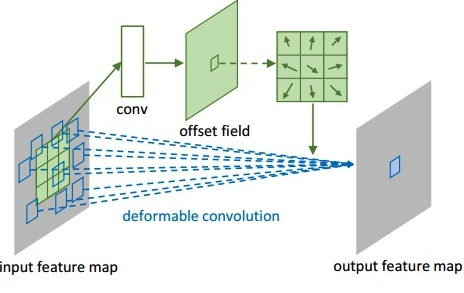
可形变卷积Paper: Deformable Convolutional Networks 可变形卷积的核心思路是:

在标准卷积的基础上增加一个分支取学习卷积核的位置偏移权重,从而得到不规则形状的卷积核,可形变卷积在提取不规则形状目标的特征比较work. 可形变卷积示例:

img

激活函数

复杂网络如果单纯由卷积层等线性单元组成的话,则最终的输出和输入始终是线性关系.

激活函数的设计在于能够将线性关系转化为非线性关系,从而实现对任意函数的拟合.各种激活函数可参考:wiki_activication

sigmoid

sigmoid为早期用得最多的激活函数,输出值的范围为(0,1),激活函数的公式为:

img

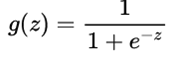
激活函数的转换关系图例:

img

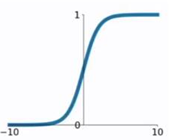
sigmoid函数的劣势是当Z值非常大或者小的时候,会导致导数趋向于零,即权重的梯度会趋近于0,即\梯度消失\现象.

tanh

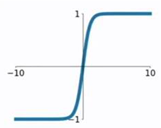
tanh函数与sigmoid函数类似,将取值(−∞,+∞) 映射到(-1,1)之间. tanh函数的公式为:

img

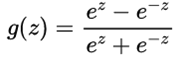
激活函数的转换关系图例:

img

ReLU以及变种

ReLU又被称为修正线性单元(Rectified Linear Unit),为非线性函数,能够一定程度上弥补sigmoid等函数梯度消失的问题 ReLU的公式如下:

img

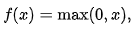
ReLU图例:

img

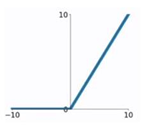
ReLU的优势在于输入为正的时候,不存在梯度消失的问题,且运行速度很快(线性),但是在输入为负的时候,会发生梯度消失的问题. 基于ReLU的变种函数很多,如:Leaky ReLU,Parameteric ReLU等,解决了ReLU函数在输入为负的情况下产生的梯度消失的问题. Leaky ReLU公式:

img

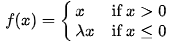
Leaky ReLU图例:

img

swish

swish是基于NAS搜索得到的激活函数,可以认为是介于线性函数和ReLU函数之间的平滑函数,效果上优于ReLU. swish函数公式如下: swish函数具备无上界有下界,平滑,非单调的特性.

img

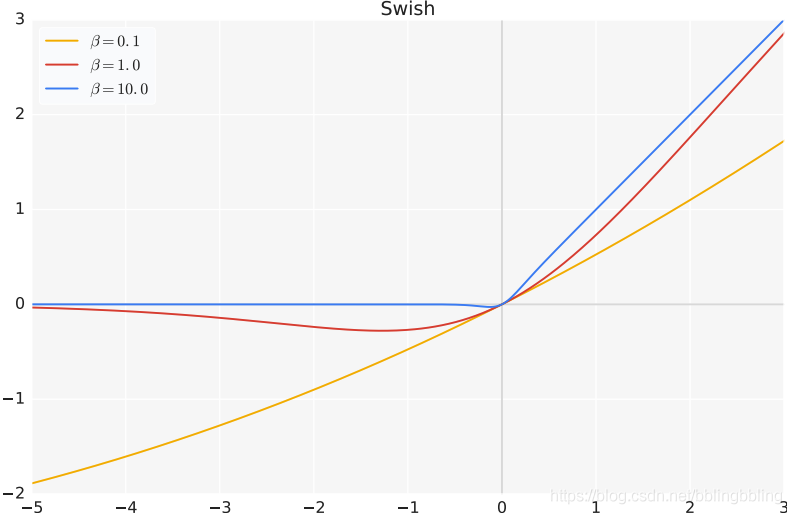
池化层

池化层的作用在于减小feature map的尺寸,减少后期网络参数量同时也防止模型的过拟合,也可认为是一种降采样的操作. 池化层一般分为两种方式:均值池化(avg pooling)和最大值池化(max pooling),avg pooling是将特征图取平均值,max pooling则取最大值. avg pooling图例:

img

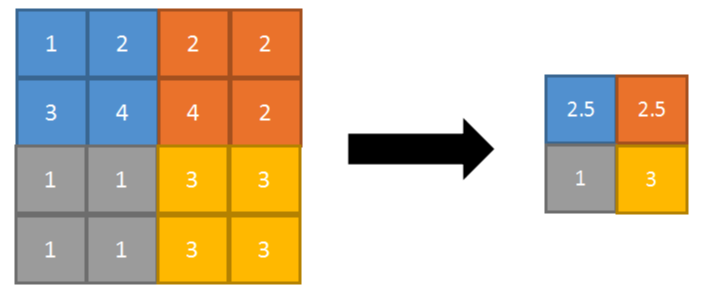
max pooling图例:

img

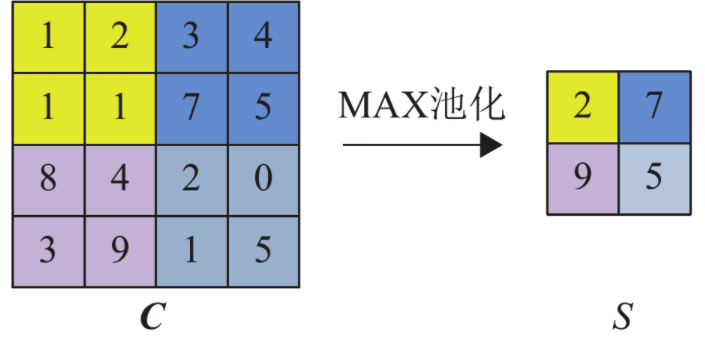
BN层

BN,全称Batch Normalization,于2015年提出:batch normalization: accelerating deep network traning by reducing internal covariate shift.

BN出现的背景在于深度学习对于归一化后的数据最优解的寻优过程会更加平稳,更容易收敛.然而如果只在数据的输入进行归一化.

在网络训练的过程中,由于参数的更新,各个网络层的数据分布发生变化.对于相邻的网络层,前层的数据分布引起后层的数据分布的变化的现象称之为”**internal covariate shift**”.

该现象会使得训练过程中个层的数据分布容易陷入饱和区,减慢网络的收敛.BN的设计正是为了解决各层的数据分布引起的网络收敛问题.

BN层的思路在于:对每一层的输入数据进行归一化操作,相对于最基本的归一化操作,BN层进行了变换重构:引入可以学习参数,主要是对归一化进行大小(scale)变换和偏移(shift)变换操作.关键函数如下:

img

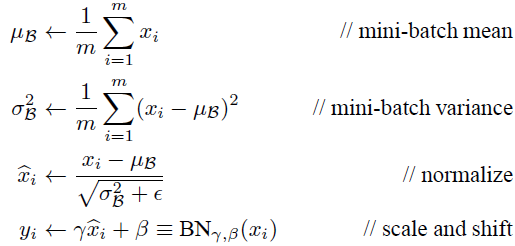
训练过程中,数据均值和方差均为每个batch中学习得到,scale和shift偏移也基于每个batch学习.infer过程中,BN的参数为固定参数,其中数据均值和标准采用训练过程所有mini batch的均值和标准差(其中标准差采用的是无偏估计结果):

img

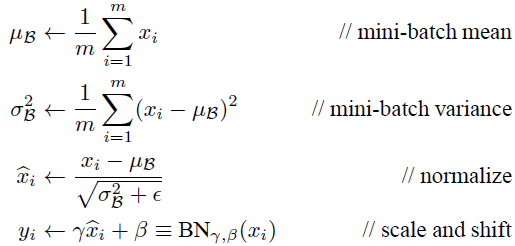
BN层的优势在于三点:

  • 缓解梯度消失,BN层可以让数据分布不在于饱和区域,实现了层间解耦,加快网络收敛
  • 简化调参,BN层使得网络训练对参数的敏感性下降,调参难度更小,可以采用更大学习率,加速收敛
  • 防止过拟合,因为训练过程中数据的均值和方差均为每个batch的数据生成,相当于加入一定的随机噪声,可以一定程度替代dropout,l2正则

BN层的缺点:

  • BN层性能与batch size有关,一般更大batch size性能稍好于小batch size性能,但是大batch size通常对显存要求较高,如fater r-cnn,通常只能采用1/2的batch size.
  • 由于测试时采用训练数据的均值/方差数据,导致训练数据较强依赖于测试数据

GN层

GN层来自facebook2018年的论文: group normalization.

其思路核心是将n通道特征分成g组,以此计算均值和方差,实现样本的归一化操作.其算法原理在于不同通道表述的特征并不是毫不关联的,几组特征往往具有同分布的性质,因此进行组内normalize是比较合理的方式.不同normalize的方式如下:

img

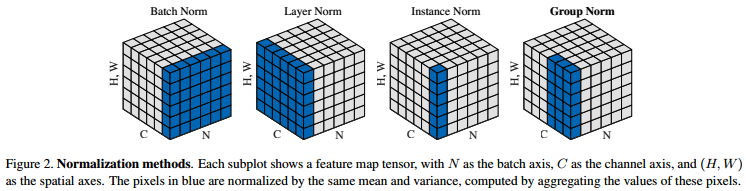
GN在batch size变小时,性能比较稳定,比BN性能要好的多.

FRN层

GN层虽然在batch size变小时性能更好,但是在正常batch size的时候,其精度不如BN.其次google于2019年提出了FRN.

img

img

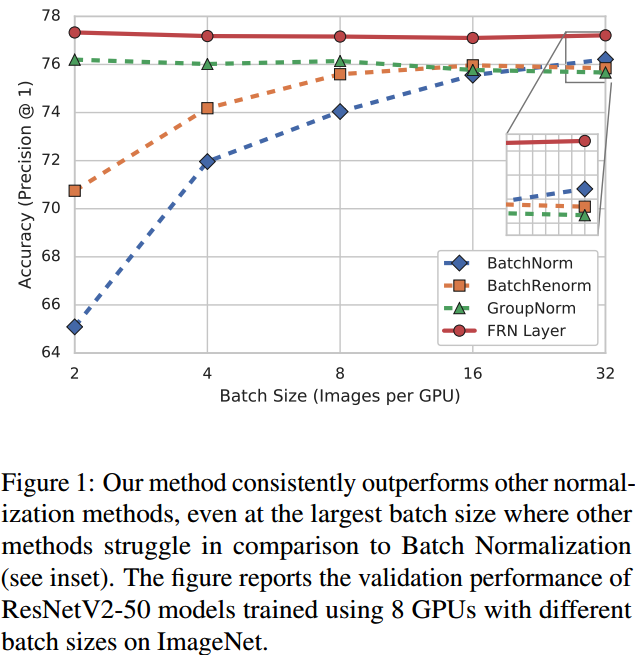
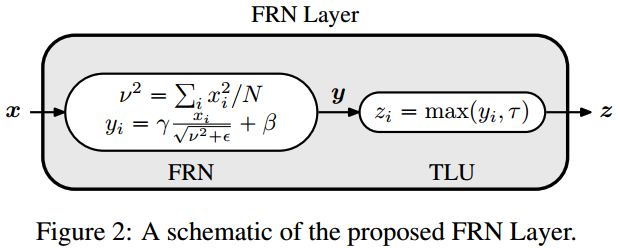
FRN分为两个部分: FRN+tlu.FRN完成的是数据的normalize操作,假设输入的shape为 (b,c,h,w) ,分别为 batch size, 通道数, 特征图的高,宽.

FRN的normalize操作不再采用均值/方差,而是采用对$h*w$​的特征值来求取平均平方和: v^2,然后采用如下的normalize方式:

上述normalize的问题在于没有减去均值,导致归一化的特征值非零对称的,如采用relu作为激活函数,则会引起误差(如很多零值),所以需要进行relu的修改,引入一个可学习的阈值 tau:

细节上,FRN层由于没有均值中心化,所以对学习率选择会较为敏感,作者建议可以采用warm-up(可参考: csdn-blog)来进行调整.

Dropout层

Dropout原理为:前向传播过程中,某个神经元的激活值以一定概率p停止工作,这样可以使得模型泛化性增强,预测过程中每个神经元的权重参数要乘以概率p,Dropout的效果如下:

img

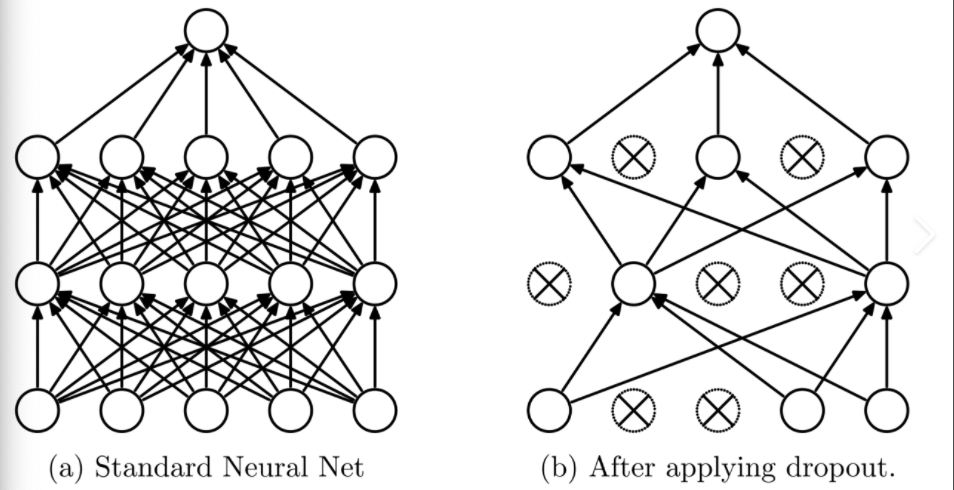
Dropout层的作用在于:

  • 多模型的平均:类似于多数投票取胜的策略
  • 减少神经元之间复杂的共适应性关系

全连接层

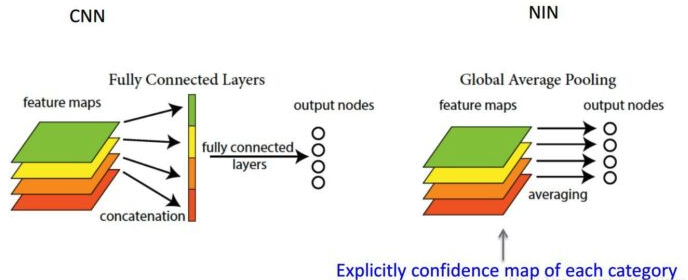
物体检测算法中,卷积网络的作用在于从局部到整体地提取图像特征,而全连接层则是将卷积得到的高维特征映射到特定维度的标签空间,以求取损失或者输出预测结果.

全连接层问题在于参数量过大,容易产生过拟合现象.后期也有很多场景使用全局池化层(GAP, Global Average Pooling)来取代全连接层. GAP的优势在于:降低网络参数量的同时降低了网络的过拟合成都,同时去除了网络输入尺寸的限制,且赋予了每层featuemap一定语义.全连接层和GAP的区别如下:

img

感受野计算

参考计算网站:fomoro ai

感受野(receptive field):

img

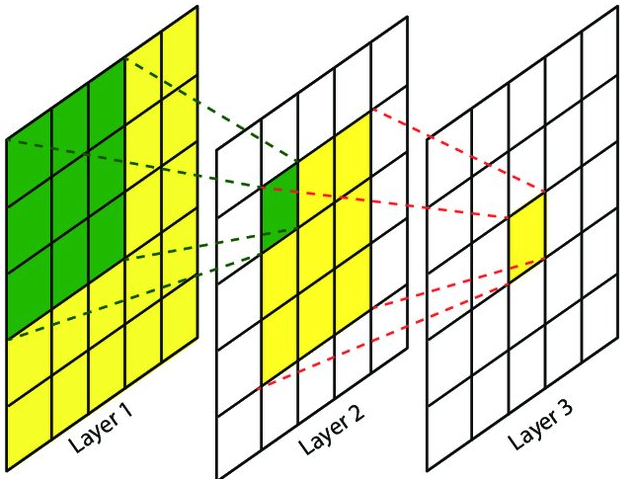
计算公式: 其中 $R_n$ 对应n层的感受野, $f_(n-1)$ 为n层卷积核大小, $s_i$为$i$层的步长

算法篇
CV 综述
This post is licensed under CC BY 4.0 by the author.
最近更新
文章目录

2D检测算法综述(2D_Detection)

2D_Detection-Backbone