算子编程模型
硬件特性
当前深度学习应用硬件主要是GPU和各类XPU(AISC),GPU架构设计上的最大的特点是:
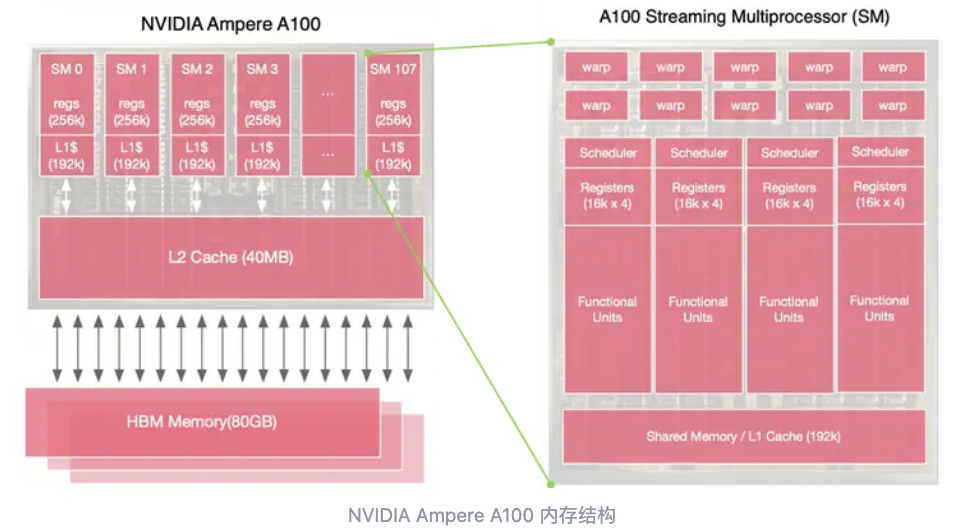
内存架构:GPU的片上Cache相对较小,且通常采用HBM等高带宽的存储,会设计多级存储方案
计算单元:GPU有强大的计算单元,且超配大量的多线程,专注大规模并行的计算任务。计算单元以GPU SM为单位,GPU单个时钟周期能支持多个Warp,A100为例,每个SM包含64个Warp,包含2048个线程。

软件特性
GPU独特的硬件设计对应其SIMT编程特性,而传统的CPU或者XPU都是SIMD编程模型,其主要区别在于:
SIMD采用一个线程处理一个指令,指令是向量化处理的,意味可以支持单指令多地址,且维度是固定的,如32bit的4维向量vec4,需要4的整数倍数据。
其优势是,对于大尺寸连续数据的处理上,SIMD性能更有优势,但是对于小数据尤其是没法保持为整数倍的数据,会有一定程度计算浪费。
SIMT采用的思路是单核多线程,即单个计算单元(SM)是支持多线程的,即多线程同指令,通过多线程的方式来降低IO的时延。
SIMT对开发人员的要求是更低的,因为SIMT始终是统一指令的,只要处理好不同线程之间的数据排布即可。
样例
以下以一个基础的矩阵乘:$C = A \times B$样例:
- 矩阵 A 的大小为 $M \times K $。
- 矩阵 B 的大小为 $K \times N $。
- 矩阵 C 的大小为 $M \times N $。
基于SIMD的实现,以Ascend C为例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// Ascend C 矩阵乘法 (GEMM) 示例
void gemm_cce(__gm__ float *A, __gm__ float *B, __gm__ float *C, int M, int N, int K) {
// 定义缓冲区大小
__ub__ float A_tile[128 * 128];
__ub__ float B_tile[128 * 128];
__ub__ float C_tile[128 * 128];
// 设置 Tile 大小 (块的大小,Ascend 推荐用 32 的倍数)
const int TILE_M = 128;
const int TILE_N = 128;
const int TILE_K = 128;
// 按块计算矩阵乘法
for (int m = 0; m < M; m += TILE_M) {
for (int n = 0; n < N; n += TILE_N) {
// 初始化 C_tile
__memset(C_tile, 0, TILE_M * TILE_N * sizeof(float));
for (int k = 0; k < K; k += TILE_K) {
// 从 GM 加载 A 和 B 的子块到 UB
__gm_to_ub(A_tile, A + m * K + k, TILE_M * TILE_K * sizeof(float));
__gm_to_ub(B_tile, B + k * N + n, TILE_K * TILE_N * sizeof(float));
// 使用向量化 Tile 计算块级矩阵乘法
for (int i = 0; i < TILE_M; ++i) {
for (int j = 0; j < TILE_N; ++j) {
for (int t = 0; t < TILE_K; ++t) {
C_tile[i * TILE_N + j] += A_tile[i * TILE_K + t] * B_tile[t * TILE_N + j];
}
}
}
}
// 将结果写回到 GM 中
__ub_to_gm(C + m * N + n, C_tile, TILE_M * TILE_N * sizeof(float));
}
}
}
基于SIMT的实现,以CUDA为例:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <cuda_runtime.h>
#include <iostream>
// CUDA 核函数:计算 C[i][j] = sum(A[i][k] * B[k][j])
__global__ void gemm_simt(const float *A, const float *B, float *C, int M, int N, int K) {
int row = blockIdx.y * blockDim.y + threadIdx.y; // 当前线程负责的行
int col = blockIdx.x * blockDim.x + threadIdx.x; // 当前线程负责的列
if (row < M && col < N) {
float value = 0;
for (int k = 0; k < K; k++) {
value += A[row * K + k] * B[k * N + col];
}
C[row * N + col] = value;
}
}
int main() {
// 定义矩阵维度
int M = 256, N = 256, K = 256;
size_t size_A = M * K * sizeof(float);
size_t size_B = K * N * sizeof(float);
size_t size_C = M * N * sizeof(float);
// 分配主机内存
float *h_A = new float[M * K];
float *h_B = new float[K * N];
float *h_C = new float[M * N];
// 初始化矩阵(略)
// 分配设备内存
float *d_A, *d_B, *d_C;
cudaMalloc((void **)&d_A, size_A);
cudaMalloc((void **)&d_B, size_B);
cudaMalloc((void **)&d_C, size_C);
// 数据拷贝到设备
cudaMemcpy(d_A, h_A, size_A, cudaMemcpyHostToDevice);
cudaMemcpy(d_B, h_B, size_B, cudaMemcpyHostToDevice);
// 定义线程和块的维度
dim3 threadsPerBlock(16, 16);
dim3 blocksPerGrid((N + threadsPerBlock.x - 1) / threadsPerBlock.x,
(M + threadsPerBlock.y - 1) / threadsPerBlock.y);
// 执行 CUDA 核函数
gemm_simt<<<blocksPerGrid, threadsPerBlock>>>(d_A, d_B, d_C, M, N, K);
// 复制结果回主机
cudaMemcpy(h_C, d_C, size_C, cudaMemcpyDeviceToHost);
// 检查结果(略)
// 释放资源
delete[] h_A;
delete[] h_B;
delete[] h_C;
cudaFree(d_A);
cudaFree(d_B);
cudaFree(d_C);
return 0;
}