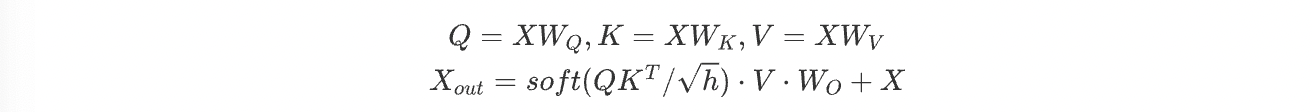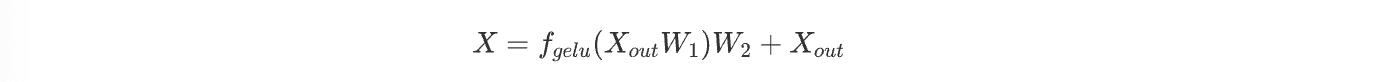前言
本文主要介绍Transformer类大模型训练/推理过程中的计算量/显存占用情况,因为对于大模型推理/训练而言,计算量决定了模型的训练/推理速度,显存占用情况决定了可供训练/推理的数据量(更大的显存能够并行跑更多的数据或者更长的序列)。 对于LLMs(Large Language Models)而言,模型结构整体趋同,整体可以分为:encoder-decoder和decoder-only两类。其中,GPT/GLM/LLaMA等主流对话类大模型都是基于decoder-only框架,且由于encoder/decoder在模型结构上差异不大,所以本文主要基于decoder-only框架进行模型参数量、计算量、显存的分析。
参数量
Decoder-only模型主要由前置 Embedding层 + L \* Transformer Block + logits 输出层组成。 其中,模型的关键参数为:
- transformer层数l
- 隐藏层维度h
- 注意力头数a
- 词表大小V
- 数据批次b
- 序列长度s
其中,主要结构为Transformer Block,Transformer Block主要分为两个部分: self-attention 和 FFN 。
self-attention模块参数包含Q/K/V的权重矩阵 $W_Q$ 、 $W_K$ 、 $W_V$ ,输出 $W_O$ 以及偏置Bias,4个权重矩阵的shape都是[h,h],偏置shape都为[h] ,Add & Norm 层参数主要包含2个可训练参数:缩放参数和平移参数,为2h,所以self-attention模块的参数量为 $4h^2+4h+2h=4h^2+6h$ 。
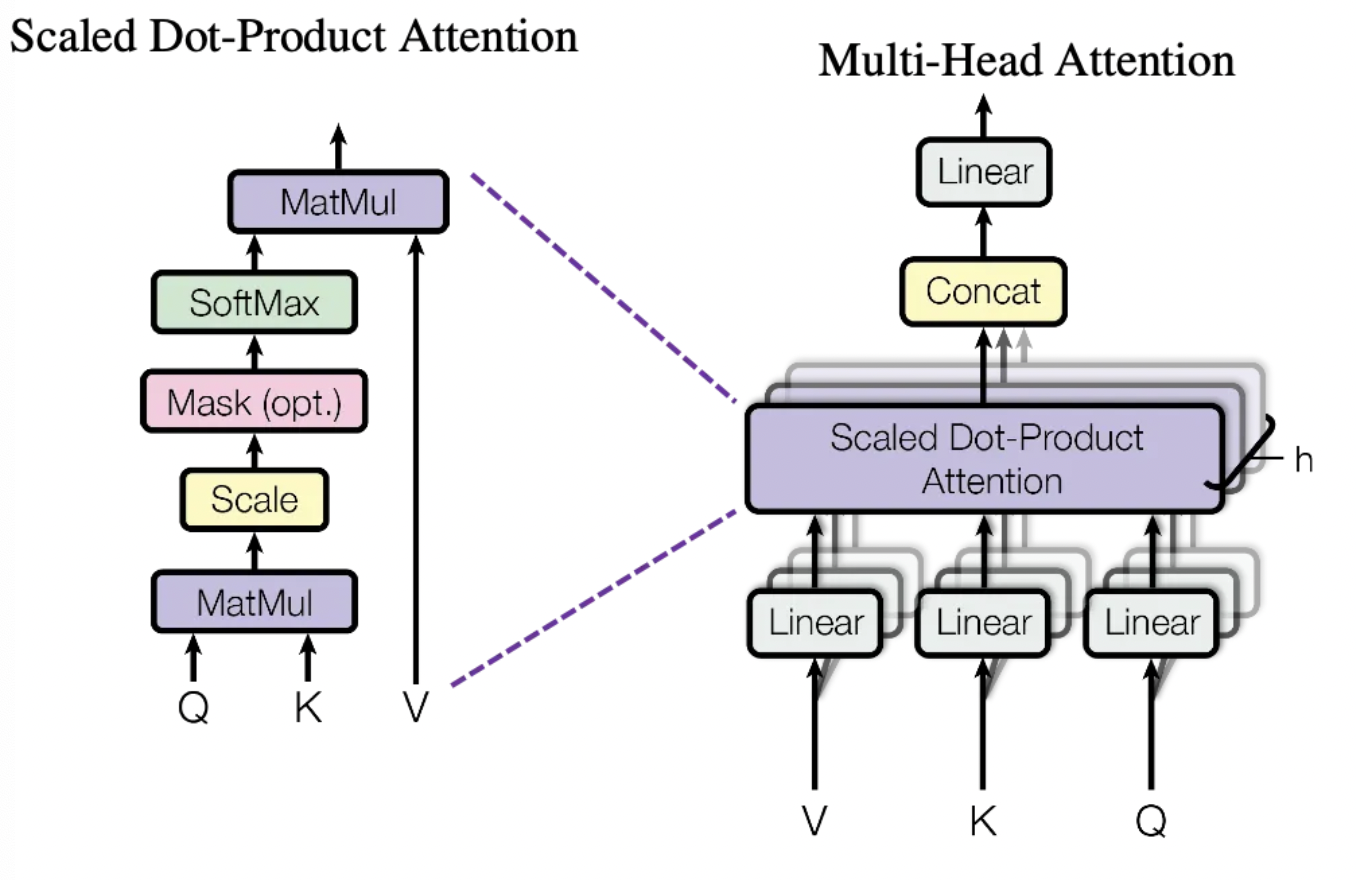
FFN层主要由2个linear层以及Add & Norm层组成,主要考虑linear层的参数量。两个linear层,分别做升维和降维操作,第一个从h->4h,第二个从4h->h。对于linear层,参数主要是矩阵权重和偏置参数,所以整体参数量为: $2*4*h*h+h+4h+2h=8h^2+7h$ 。
综上,每个trasformer层的参数量为 $12h^2+13h$ ,所以l层transformer层的参数为 $l(12h^2+13h)$ ,注意这里省略了一些参数,如位置编码,但是这部分参数通常比较少。
其他两层:Embedding层参数主要由词表维度V和隐藏层维度h决定:Vh。最后层的logits输出层主要为单个linear层和Softmax层,输出层的linear层矩阵参数通常和Embedding测光参数复用。所以这两层的参数量通常为Vh。因此整个模型的可训练参数为 $l(12h^2+13h)+Vh$ ,当隐藏层维度h较大时,可以忽略一次项,即: $12lh^2$ 。以LLama为例:
| 实际参数量 | 隐藏层h | 层数l | 参数量12lh^2 |
| 6.7B | 4096 | 32 | 6442450944 |
| 13.0B | 5120 | 40 | 12582912000 |
| 32.5B | 6656 | 60 | 31897681920 |
| 65.2B | 8192 | 80 | 64424509440 |
计算量
计算量通常以FLOPS(floating point operations)作为指标。以矩阵乘为例:对于A/B矩阵而言,A矩阵维度为1xn,B矩阵维度为nx1,计算A @ B矩阵乘需要n次乘法运算和n次加法运算,共2n次浮点运算,即2n的FLOPS;则对于mxn的A矩阵,和nxk的B矩阵,则计算的浮点运算次数为2mnk次。
对于LLMs的计算量而言,先以单次推理过程来分析:
假设输入数据的维度为[b, s],经过embedding层得到[b, s, h],词表维度V,矩阵乘的输出shape为 $[b, s, V] x [V, h] -> [b, s, h]$ ,则计算量为2bshV。
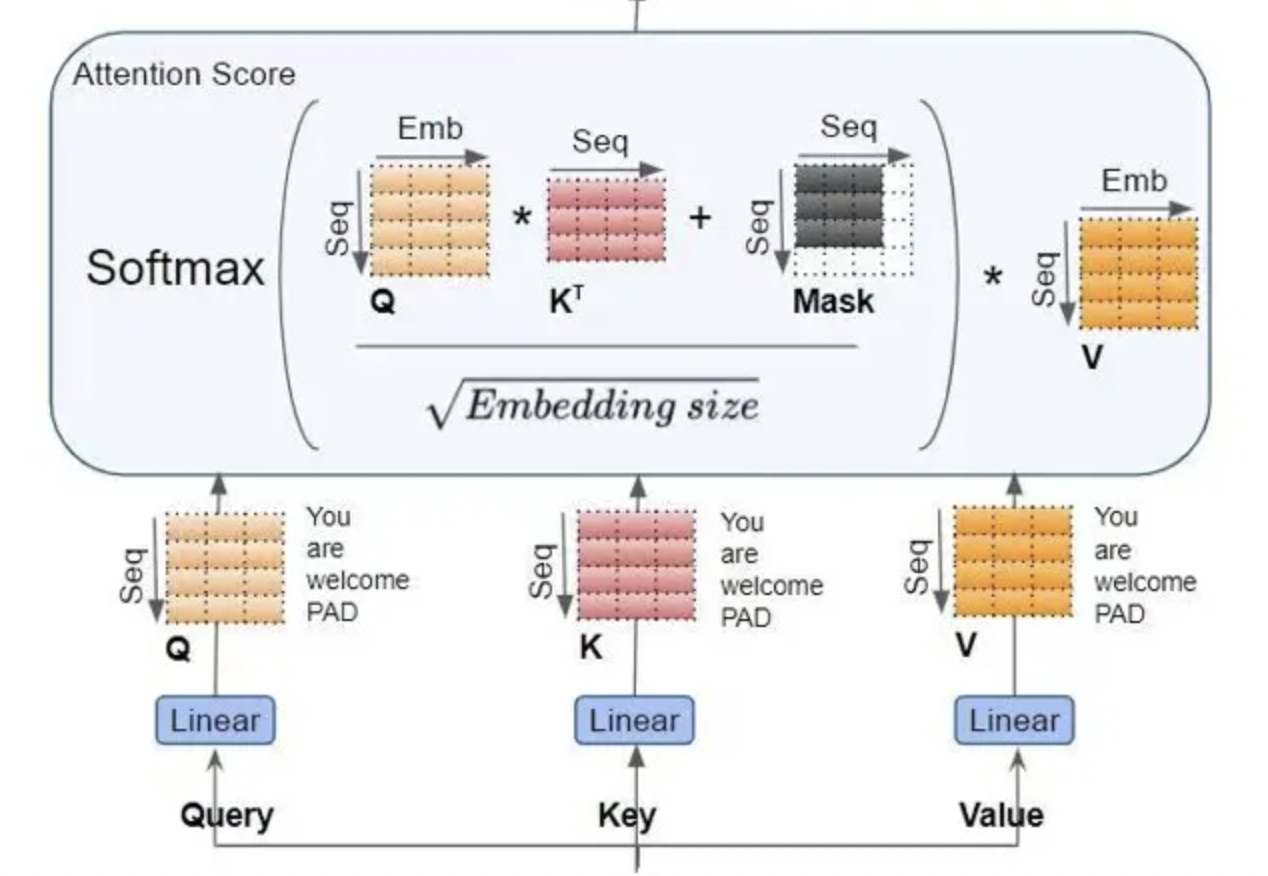
对于self-attention部分而言:
- Q/K/V三个矩阵乘的输入输出形状分别为:[b, s, h] x [h, h] -> [b, s, h],则计算量为 $6bsh^2$
- $QK^T$ 矩阵乘的输入输出形状为[b, a, s, per_head_hidden_size] x [b, a, per_head_hidden_size, s] -> [b, a, s, s],计算量为 $2bhs^2$ 。
- score \* V,矩阵乘的输入和输出形状分别为:[b, a, s, s] x [b, a, s, per_head_hidden_size] -> [b, a, s, per_head_hidden_size],计算量为 $2bhs^2$
- attention后的线性层,输入输出为[b, s, h] x [h, h] -> [b, s, h],计算量为 $2bsh^2$
取和为 $8bsh^2 + 4bhs^2$ 。
对于FFN层,两个linear层的输入输出shape分别为:
- [b, s, h] x [h, 4h] -> [b, s, 4h],计算量为 $8bsh^2$
- [b, s, 4h] x [4h, h] -> [b, s, 4h],计算量为 $8bsh^2$
取和为 $16bsh^2$ 。
最后计算logits中,矩阵乘的输入输出shape为:[b, s, h] x [h, V] -> [b, s, V],计算量为2bshV。
综上,整晚前向推理的计算量为: $l(24bsh^2 + 4bhs^2) + 4bshV$ 。当前隐藏层维护h比较大时(远大于序列s时),可以忽略一次项: $24lbsh^2$ 。前置可知模型参数量为 $12lh^2$ ,假设输入tokens数目为bs,则存在 $24lbsh^2 / (12lbsh^2) = 2$,即在推理过程中,可近似认为单个token,单个参数,需要进行两次浮点运算。
对于训练而言,除了前向推理外,还包含反向梯度计算/参数更新两步,即反向过程为前向过程计算量的2倍。所以对于训练任务而言,每个token,单个参数,近似需要进行6次浮点计算。
显存占用
模型推理过程中,显存占用主要分为两个部分:模型参数、前向推理的中间激活值;对于训练来说,还有后向传递的梯度、优化器状态。这里的优化器以大模型训练最常用的AdamW优化器为例,且默认以混合精度训练分析。
单次训练迭代过程中,每个可训练参数都对应一个梯度和2个优化器状态(一阶/二阶动量)。对于混合精度而言,计算过程中(前向推理/反向梯度计算),权重/梯度都以FP16/BF16,对应2个bytes,但是反向参数更新过程中需要备份数据且转换为FP32精度,对应4个bytes;AdamW状态器都存为FP32,所以对于单个参数而言,其显存占用为:$2+4+2+4+4+4 bytes$ 。
前向推理过程中,主要为模型参数和中间激活值。这里忽略一些小buffers,如embedding层、输出层等,因为在h较大,l较深情况下这部分层的中间激活值很少。所以中间激活值主要为l层transformer层:
self-attention

计算Q/K/V,需要保存X,输入X的形状为[b, s, h],dtype为FP16/BF16,占用显存为2bsh
计算 $QK^T$ ,Q/K矩阵两个张量为[b, s, h],总共为4bsh
计算softmax,需要保存 $QK^T$ ,总共为 $2bs^2a$
dropout的mask:shape同 $QK^T$ 一致,dtype为bool,占显存 $bs^2a$
计算attention,需要保存score值/V,分别为 $2bs^2a+2bsh$
计算输出映射以及dropout,保存X以及mask,分别为 $2bsh+bsh$
综上,总和为 $5bs^2a+11bsh$ ,但是注意的是:实际在纯推理过程中,部分tensor可以复用。
FFN

第一个线性层的输入,显存占用为2bsh
激活函数需要保存输入,显存占用为8bsh
第二个线性层的输入,显存占用为8bsh
dropout的mask输入,为bsh
总和为19bsh,另外还存在两个normalization层,需要保存输入为中间激活层,分别为2bsh,总共为4bsh。
综上,对于l层transfromer模型,中间激活占用的显存近似为 $l(5bs^2a+34bsh)$ 。
另外,对于LLM单推理过程中,通常会采用KV Cache的方式来进行推理加速,对于KV Cache而言,其主要分为两个部分:
- 预填充阶段:输入一个prompt序列,为每个transformer层生成key cache和value cache,大小和输入prompt序列数据一致
- 解码阶段:使用并更新KV cache,一个接一个生成词,这里通常有2种方式:一种通过concat的方式动态增加cache值;另一种,提前申请最大的cache,通过偏移进行更新,避免动态申请降低性能。
假设输入序列长度为s,输出序列长度为n,以FP16/BF16保存KV Cache,则KV Cache的峰值显存占用为 $b(s+n)h*l*2*2=4blh(s+n)$ ,其中第一个2表示K/V值,第二个2为bytes。