前言
浅谈 Transformer 原理以及基本应用以及模型优化的一些思考。
Transformer介绍
Transformer 最早出自Google 2017年发布的论文:Attention is all you need。Transformer 结构提出在于完全摈弃了传统的循环的”encoder-decoder”结构,取而代之的是采用”self-attention”结构。传统的循环结构的问题在于:结构是串行的,即下个结构的输入依赖于上层结构的输出,该固有属性的问题是该”encoder-decoder”结构无法进行并行推理,效率较低。而基于”Attention”结构,能够很好的解决该问题,其基本结构如下:
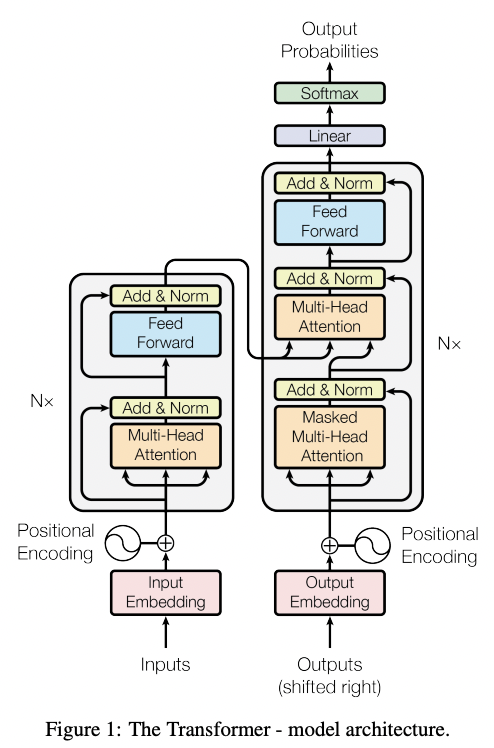
上述自注意机制的核心是通过某种计算来直接得到句子在编码过程中的每个位置的注意力权重;然后再以权重和的形式来计算得到整个句子的隐含向量表示。所谓自注意机制即文中的”Scaled Dot-Product Attention”,其核心在于将query和一系列的key-value对映射到某个输出的过程,而该输出向量本质上是基于query/key得到权重然后作用于value的权重和:
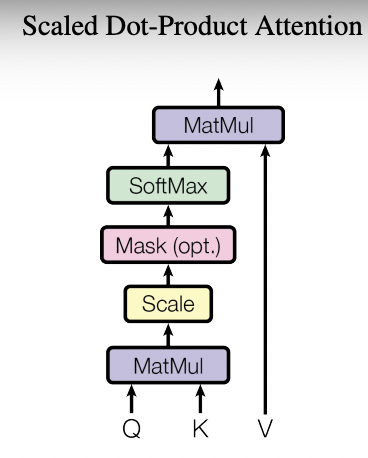
基于上文结构可以得到基于该结构的输入:Q/K/V,其输出向量为:
\[Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V\]其中, $Q/K/V$ 分别对应三个输入矩阵,其中的维度为: $d_q,d_k,d_v$ 。 其中, $Q/K/V$ 可以认为是输入向量通过不同的 embedding 方式得到的三个输入向量(即对应不同权重得到的不同映射输入),$QK^T$ 得到是序列不同元素间的注意力权重,最后再将该注意力权重作用于 $V$ 即得到最终的编码输出。另外, $d_k$ 的引入主要是为了防止softmax后梯度过小,即 scaled 的过程。该结构的优势是能够直接通过多次矩阵变换便得到序列输入各自元素间的编码向量。
但是仍然存在一系列的问题,首先上述”自注意力机制”的问题在于:模型低当前位置的信息进行编码时,会过度地将注意力集中在自身位置上;同时,上述编码机制的问题在于其对位置是不敏感的,即元素的前后输入顺序关系不同,编码的值仍然是不变的,只是输出位置和输入位置保持一致,即无法捕获输入顺序引起的本身语义的差异。
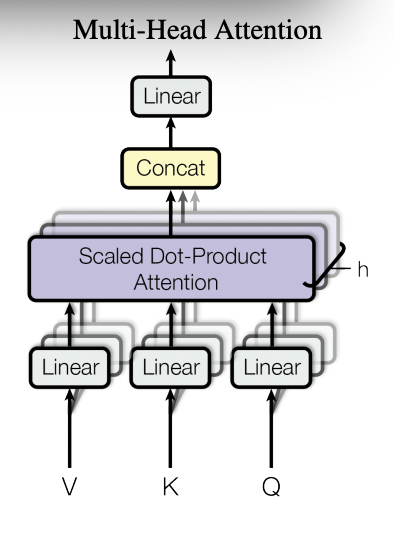
对于第一个问题,作者采用了”Multi-Attention”结构。从下文的结构中可以看出,其结构本质上将原始的输入序列进行多组的自注意力处理过程,然后将每一组自注意力结果进行拼接然后进过一次线性变换得到最终的输出结果。对于多头结构,其核心在于将原始的高维的单头结构,分解为不同权重得到的多个低维结果(但在计算实现上两者等价)。增加多头的优势在于提高模型的表达能力(类似CV场景上多组滤波器的设计),现象上看能增加对其他位置信息的注意力权重,减缓对自身位置过于关注的问题;另一方面多头的设计提高了模型的并行度。
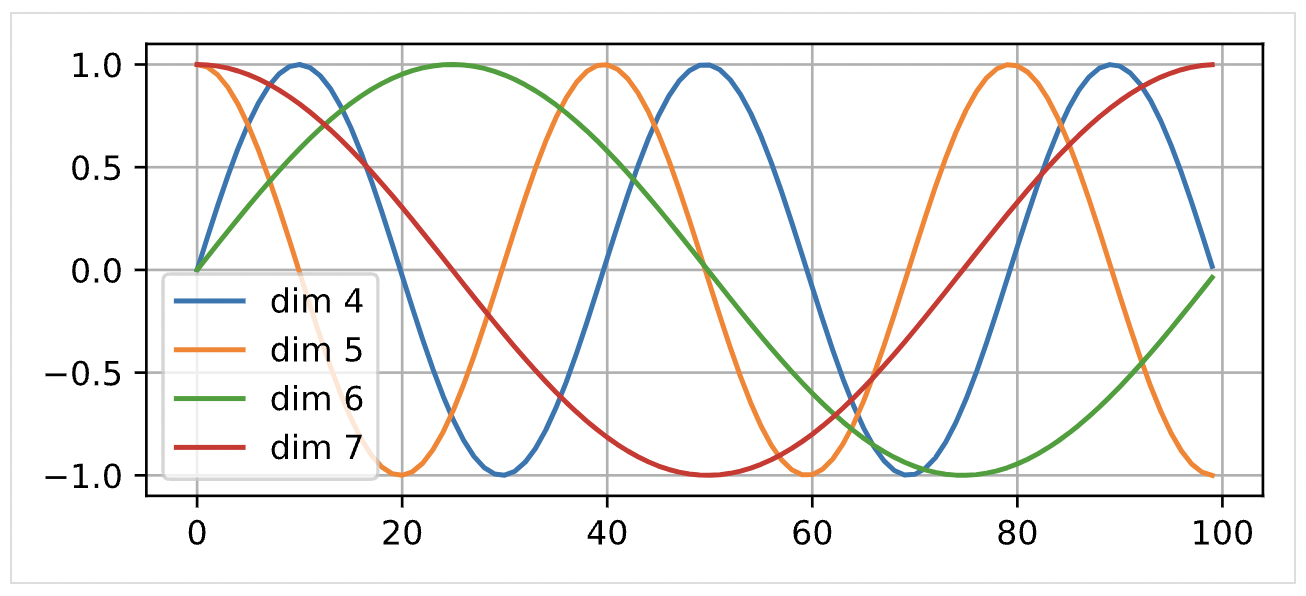
对于输入位置的问题,作者额外加入了一个 Positional Embedding 特征用于刻画数据在输入时序上的差异。关于 Positinal Embedding 可以参照下图,其中横坐标表示输入序列顺序的位置信息,不同位置能够通过某种公式变换得到特定的输出结果。
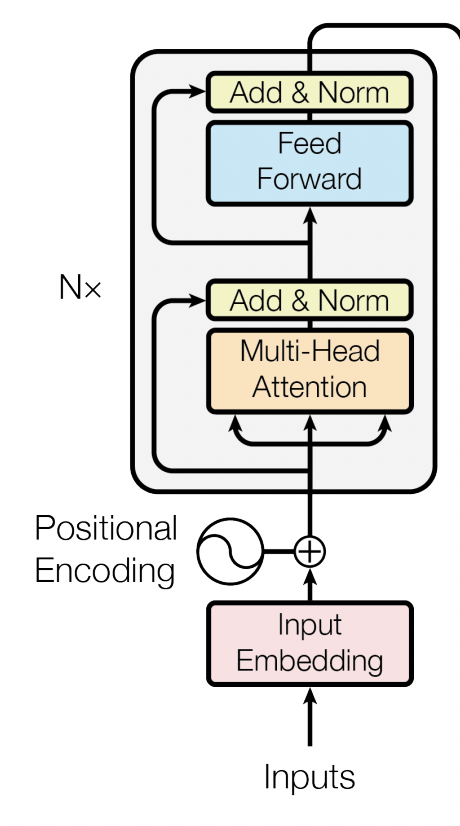
介绍完 Multi-Attention 结构,可以发现 Encoder 结构主要由两部分组成: Multi-Attention 和 Feed Forward (两层全连接网络)。其中每个部分均为 LayerNorm(x+Sublayer(x)) ,并且都加入了 Dropout 操作。另外对于 Feed Forward 部分来说,其计算过程可以归纳为:
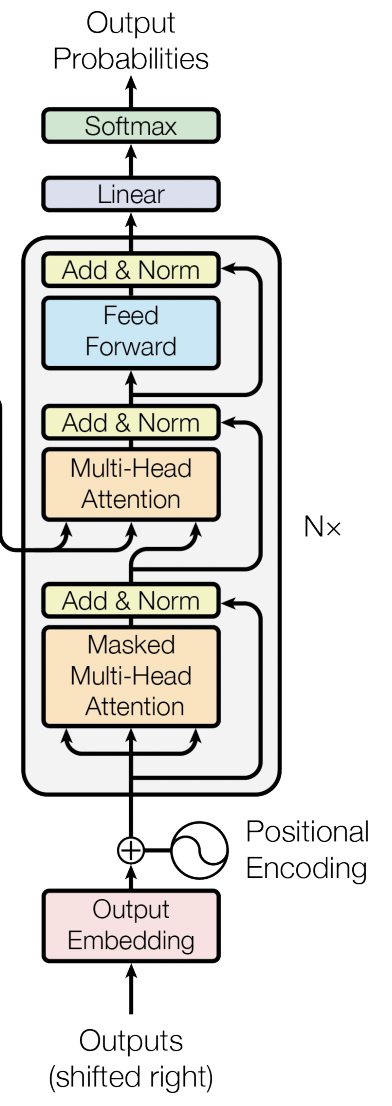
Decoder结构整体上和Encoder结构类似,区别在于多了一个用于和Encoder输出进行交互的多头注意机制(memory输入得到K/V,Q来自自身结构的输入)。其核心在于将Encoder得到的memory权重信息用于自身的解码操作。
最后谈下 Transformer 的掩码机制:
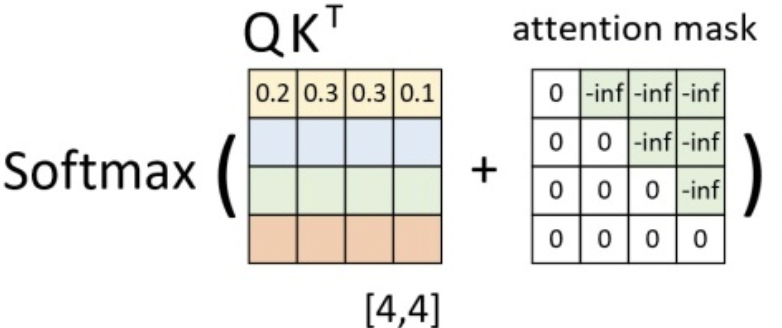
在真实预测时解码器需要将上一个时刻的输出作为下一个时刻解码的输入,然后一个时刻一个时刻的进行解码操作。显然,如果训练时也采用同样的方法那将是十分费时的。因此,在训练过程中,解码器也同编码器一样,一次接收解码时所有时刻的输入进行计算。这样做的好处,一是通过多样本并行计算能够加快网络的训练速度;二是在训练过程中直接喂入解码器正确的结果而不是上一时刻的预测值(因为训练时上一时刻的预测值可能是错误的)能够更好的训练网络。基于上述情况,”掩码机制”很好地解决了该问题,其原理是在 $QK^T$ 的基础上添加掩码: $QK^T + attention_{mask}$ 。其作用是能够保证在解码 $t$ 时刻的时候,只能将注意力放在前 $t$ 个位置。
Transformer for CV
Transformer 通常被应用于NLP等领域,特点是输入通常为序列,这也与其模型结构相互对应。但是,后续也有很多的研究投入到 Transformer 应用到CV领域。 相对于常规卷积算子, Transformer 的优势在于:
- 能够突破位置距离(感受野)的限制,因为对于
Transformer来说,计算两个位置之间的关联所需要的操作次数不随距离增长 self-attention的结构更具有解释性,可以获取各个attention head的注意力分布- 更强的建模能力:Transformer的核心是描述”query”和”key”的关系,可以应用与像素值和位置的关系(类似于卷积),同样也可以描述其他输入的关系。因此,Transformer结构能够应用于更多领域,或者说联通不同领域,构建更泛化的模型。
并行计算:计算效率高(尚待商榷,因为transformer类网络结构往往在硬件实现上存在内存访问不友好等问题,所以同样计算量的模型,可能transformer类型网络却要慢得多)
对于CV领域,运用
Transformer的核心思路是 将图片编码为序列 , 一般步骤为:特征提取(通常基于CNN)和下采样(降维)
进行
position encoding与图片特征结合,得到输入序列将序列送入
transformer block设计特定的
task head: 分类/检测/分割等任务
以下介绍几个经典应用及其网络结构:
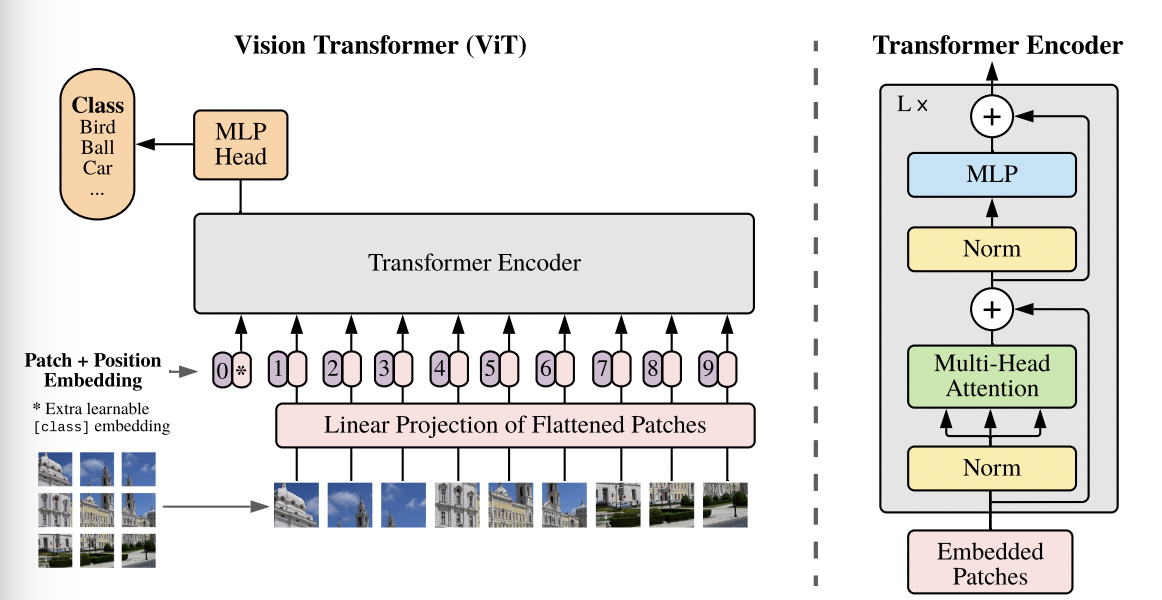
- 分类任务 Vision Transformer (ViT) 将
Transformer应用到图像分类,其核心网络结构见下图,其算法流程为:- 图像分块:将原始HxWxC的图像分为PxPxC的patches,然后进行展平为序列,序列长度为 $Nx(P^2xC)$,其中N为patch数目
- patch embedding: 类似于NLP的embedding操作,实际是进行高维度向量向低维度向量的转换。这里采用了券链接层,最后得到的维度为ND;另外这里还追加了一个分类向量,主要用于描述各个patch的分类信息。最后加入位置编码(position encoding)信息
- 将得到的embedding后的序列输入到
encoder-decoder结构中 - 分类head:基于MLP实现。

检测任务
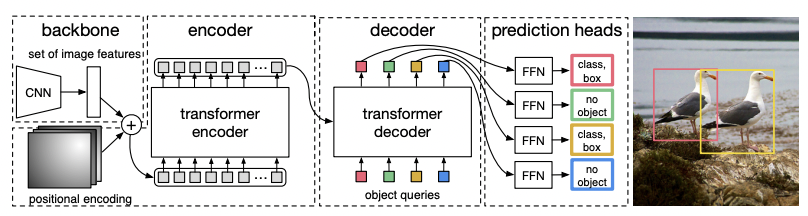
DEtection TRansformer (DETR),其算法结构见下图,其核心算法步骤如下:
类似于ViT,先对图像进行分块,然后基于CNN和positional encoding得到输入序列
将得到的输入序列作为transformer结构的输入
检测head:核心结构,论文称为
FNN:对于各个decoder的输出,不同的FFN其实是权重共享的。内部结构包括两个部分:ReLU激活的三层感知机进行边框预测+线性层+Softmax预测分类。match机制以及loss设计:最终网络的得到的预测结果实际上是个集合(集合大小为N),集合元素为: $(probs, bbox)$ ,表示检测框的类概率以及检测框坐标。与GT的匹配计算loss时,采用的匹配机制为匈牙利算法,Loss采用的是
Hungarian Loss,其核心最小化匹配的损失。

分割任务
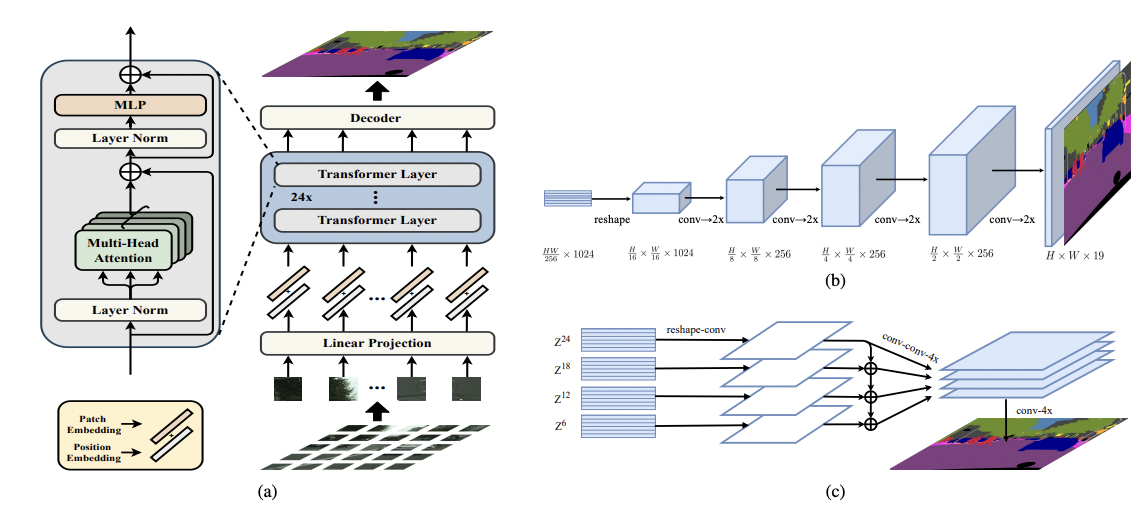
SEgmentation TRansformer (SETR),其算法结构见下图,整体算法步骤上看,大同小异:
构造输入,得到各个patch的特征,然后编码空间信息,组合为最终序列
输入
transformer结构进一步decoder得到最终分割结果,论文介绍了两种decoder结构: (b),reshape为图片维度后不断通过卷积进行上采样;(c)不同层的feature进行提取,然后合并提取(multi-level feature aggragation)最终的输入。

通用骨干网络
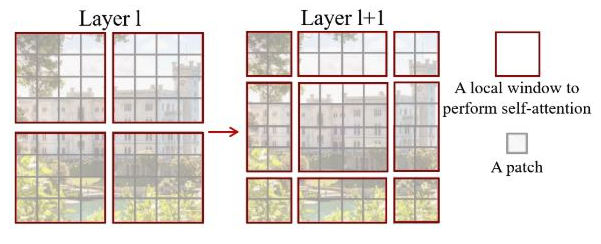
Swim-transformer一定程度可以认为是
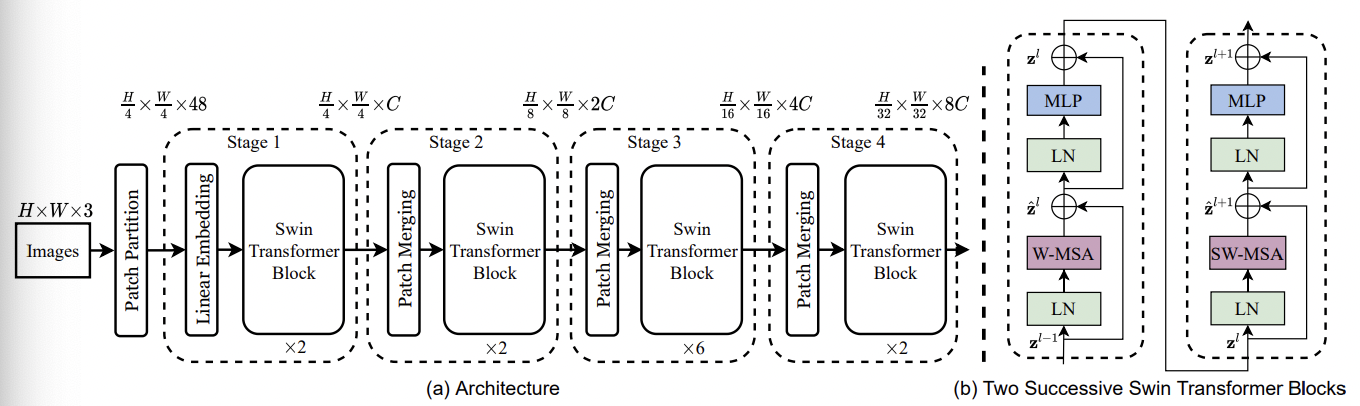
transformer类型的集大成者,其网络结构见下图。基于Swim-transformer的网络在各个任务上的都达到了SOTA的精度。除了常规的视觉任务(物体检测和语义分割等),其在其他任务上也表现亮眼,如:视频动作识别,自监督学习,图像复原,ReID等,个人认为Swim-transformer的算法设计还是极具创新性的,该论文也为2021 ICCV Best Paper(上一次MSRA拿到Best Paper的时候还得追溯到ResNet了)。先谈谈前面基于
Vit的网络结构的缺陷:基于分块的输入维度很高: $patch^2$ ,时间复杂度高
输入序列长度单一:对于CV任务来说,多尺度的信息往往是重要的
Swim-transformer一定程度上解决了上述问题:将时间复杂度降至线性
能够提取多尺度的信息
Swim Transformer对CNN的降维打击这篇博客对
Swim-transformer进行较为详尽的描述,这里简单归纳狭隘其核心算法流程:输入为原始图片输入,输入到
Patch Partition模块,该模块的作用是实现图像输入的patch处理:将输入图片以大小为4x4的尺寸进行切分得到 $\frac{H}{4}\frac{W}{4}48$ 的输入,其中48对应的是: $48=443$输入到Stage1:
Linear Embeding+Swim transformer Block结构,其中Linear Embeding模块实现的是降维操作,降维48到C维度,然后输入到Swim transformer Block结构。后者为该算法的核心模块,分为连续两个部分:以W-MSA为主体的结构+以SW-MSA为主体的结构。其中W-MSA主体结构的功能是:将输入切分为不同window,然后仅在window内进行self-attention 计算(降低了计算复杂度),但是一定程度上丢失了不同window间的信息交互;SW-WSA主体结构用于解决不同window间的信息交互问题,且核心是将不同patch部分进行移动拼接为不相邻的windows之间引入连接。输入到后续结构:Stage2-Stage4:
Patch Merging+Swim transformer Block结构,其区别主要在于前置的Patch Merge模块,其功能是将输入按照2x2的方式进行合并,类似与pooling的操作,从而能够提升特征的感受野,实现不同尺度特征的提取。

补充内容:
W-MSA结构,其算法示意图如下,其中红色区域为window,灰色区域为patch。对于hxw的patches(patch大小为MxM),W-MSA结构仅对单个Window内部进行self-attention操作,所以其计算复杂度为 $4hwC^2 + 2M^2hwC$ ,与patches数目(hxw)呈线性关系;而对于Vit类型的计算方式,其计算复杂度为 $4hwC^2+2(hw)^2C$ ,其与patches数目的平方呈线性关系。

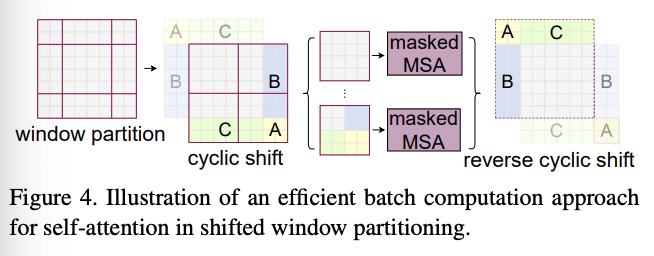
SW-MSA结构,其算法示意图如下,其核心为
cyclic shift和reverse cyclic shift操作。